Question

Two parabolas have the same axis and tangents are drawn to the second from points on the first; prove that the locus of the middle points of the chords of contact with the second parabola all lie on a fixed parabola.

Answer 1

Hint: Draw tangents from the outer parabola to the inner. Check where the tangents touch the inner parabola and find the midpoint of these points.

Complete step-by-step answer:

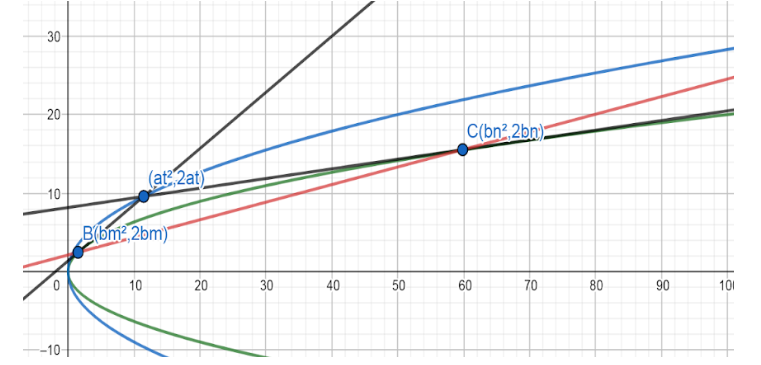
Consider the above picture.
There are two parabolas blue$\left( {{y}^{2}}=4ax \right)$and green$\left( {{y}^{2}}=4bx \right)$
From point $A$ (parameter $t$) on the blue parabola, two black tangents to the green parabola are drawn. These tangents touch the green parabola at points $B$ (parameter $m$) and $C$ (parameter $n$).
We have to find the locus of mid points of the chord $BC$.
Since $AB$ and $AC$ are tangents to the green parabola, we can write their equations using the parametric form of tangent which is $ty=x+a{{t}^{2}}$, where $t$ is the parameter of the point where it touches the parabola.
So we write equations of $AB$ and $AC$,
$AB:my=x+b{{m}^{2}}...(i)$
$AC:ny=x+b{{n}^{2}}...(ii)$
Since these two lines intersect at $A$, by solving the above equations together we will get point $A$.
Subtracting equation $(i)$ from $(ii)$i.e. $\left( ii \right)-\left( i \right)$ we get,
$\left( ny \right)-\left( my \right)=\left( x+b{{n}^{2}} \right)-\left( x+b{{m}^{2}} \right)$
$ny-my=b{{n}^{2}}-b{{m}^{2}}$
$y(n-m)=b({{n}^{2}}-{{m}^{2}})$
$y(n-m)=b(n-m)(n+m)$
$y=b(n+m)...(iii)$
Substituting equation $\left( iii \right)$ in $\left( i \right)$we get,
$n(b(n+m))=x+b{{n}^{2}}$
$bn(n+m)=x+b{{n}^{2}}$
$b{{n}^{2}}+bnm=x+b{{n}^{2}}$
$bnm=x$
$A:\left( bmn,b\left( m+n \right) \right)$
Also$A$ lies on the green parabola, so it must satisfy its equation i.e. $\left( {{y}^{2}}=4ax \right)$.
So,
${{\left( b\left( m+n \right) \right)}^{2}}=4a\left( bmn \right)...(iv)$
To find the locus of a point, we consider a point with coordinates$\left( h,k \right)$, which is a general point on the locus.
Since $\left( h,k \right)$lies on the locus which is the locus of midpoints of the chord of the parabola.
Using midpoint formula we can write,
Xmid=$\dfrac{x1+x2}{2}$
ymid= $\dfrac{y1+y2}{2}$
Therefore,
h=\left\\{ \dfrac{\left( x~coordinate~of~A \right)+\left( x~coordinate~of~B \right)}{2} \right\\}
k=\left\\{ \dfrac{\left( y~coordinate~of~A \right)+\left( y~coordinate~of~B \right)}{2} \right\\}
h=\left\\{ \dfrac{\left( \text{b}{{\text{m}}^{2}} \right)+\left( b{{n}^{2}} \right)}{2} \right\\}
$2h=\left( \text{b}{{\text{m}}^{2}} \right)+\left( b{{n}^{2}} \right)$
\dfrac{2h}{b}=\left\\{ {{\text{m}}^{2}}+{{n}^{2}} \right\\}...(v)
k=\left\\{ \dfrac{\left( 2bm \right)+\left( 2bn \right)}{2} \right\\}
$k=bm+bn$
\dfrac{k}{b}=\left\\{ m+n \right\\}...(vi)
So our next task in finding the locus is eliminating the variables from the above equations.
Squaring equation$\left( vi \right)$and subtracting it from $\left( v \right)$ i.e. ${{\left( vi \right)}^{2}}-\left( v \right)$
Which gives,
{{\left( \dfrac{k}{b} \right)}^{2}}-\dfrac{2h}{b}={{\left( m+n \right)}^{2}}-\left\\{ {{\text{m}}^{2}}+{{n}^{2}} \right\\}
{{\left( \dfrac{k}{b} \right)}^{2}}-\dfrac{2h}{b}=\left( {{m}^{2}}+{{n}^{2}}+2mn \right)-\left\\{ {{\text{m}}^{2}}+{{n}^{2}} \right\\}
${{\left( \dfrac{k}{b} \right)}^{2}}-\dfrac{2h}{b}=2mn...(vii)$
Substituting equations $\left( vi \right),\text{ }\left( vii \right)$ in $\left( iv \right)$we get,
${{\left( b\left( \dfrac{k}{b} \right) \right)}^{2}}=2ab\left( {{\left( \dfrac{k}{b} \right)}^{2}}-\dfrac{2h}{b} \right)$
${{\left( k \right)}^{2}}=2ab\left( \left( \dfrac{{{k}^{2}}}{{{b}^{2}}} \right)-\dfrac{2h}{b} \right)$
${{\left( k \right)}^{2}}=\left( \left( 2a\dfrac{{{k}^{2}}}{b} \right)-8ah \right)$
${{k}^{2}}=2a\dfrac{{{k}^{2}}}{b}-8ah$
This is the required locus.
Now since $\left( h,k \right)$are general points on our locus we can replace $h$ by $x$ and $k$ by $y$.
$\left( \dfrac{2a}{b}-1 \right){{y}^{2}}=8ax$
This is the required locus which represents another parabola.

Note: Students have to think carefully while deciding which is the variable before eliminating. In this question students might eliminate $a$ which will give them the wrong answer. Also they may use their different techniques to eliminate the variable from the equations. Also, if they feel it is redundant to use $\left( h,k \right)$ first and then replace it as $\left( x,y \right)$ they may use $\left( x,y \right)$ from the start as well.