Question

Two parabolas have a common axis and concavities in opposite directions. If any line parallel to the common axis meets the parabolas in and , prove that the locus of midpoint of is another parabola, provided that the latera recta of the given parabola are unequal.

Answer 1

Hint: Equation of line parallel to the common axis is given by $y=c$.
Let’s consider the two parabolas ${{y}^{2}}=4ax$ and ${{y}^{2}}=-4bx$.
From the equation of the parabola, we can see that the axis of the parabolas is common and their concavities are opposite.

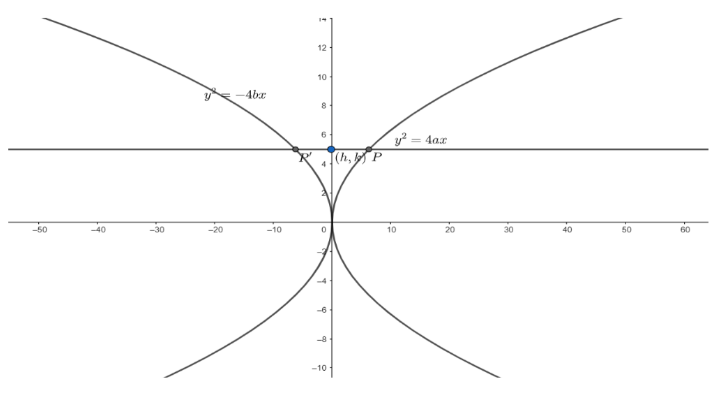
Now, we know the equation of the common axis is $y=0$.
So, the equation of a line parallel to the common axis is $y=c$.
Now, this line meets the parabolas ${y}^{2}=4ax$ and ${y}^{2}=-4bx$ at $P$ and ${{P}^{'}}$ respectively.
Let the midpoint of $P{{P}^{'}}$ be $\left( h,k \right)....\left( i \right)$.
Now, substituting $y=c$ in ${y}^{2}=4ax$, we get:
${{c}^{2}}=4ax$
$\Rightarrow x=\dfrac{{{c}^{2}}}{4a}$
So, the point $P$ is $\left( \dfrac{{{c}^{2}}}{4a},c \right)$.
Substituting $y=c$ in $y=-4bx$, we get:
${{c}^{2}}=-4ax$
$\Rightarrow x=\dfrac{-{{c}^{2}}}{4b}$
So, the coordinates of ${{P}^{'}}$ are $\left( \dfrac{-{{c}^{2}}}{4b},c \right)$.
Now, know that the coordinates of the midpoint of the line joining two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given as:$\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
So, the midpoint of $P{{P}^{'}}$ is
$\left( \dfrac{\dfrac{{{c}^{2}}}{4a}-\dfrac{{{c}^{2}}}{4b}}{2},\dfrac{c+c}{2} \right)$
$=\left( \dfrac{{{c}^{2}}}{8a}-\dfrac{{{c}^{2}}}{8b},c \right)....\left( ii \right)$
From $\left( i \right)$and $\left( ii \right)$, we can conclude that
$h=\dfrac{{{c}^{2}}}{8a}-\dfrac{{{c}^{2}}}{8b}$ and $k=c$
Or, $h=\dfrac{{{k}^{2}}}{8a}-\dfrac{{{k}^{2}}}{8b}$
Or, $h=\dfrac{{{k}^{2}}}{8}\left( \dfrac{1}{a}-\dfrac{1}{b} \right)$
Or, $h=\dfrac{{{k}^{2}}}{8}\left( \dfrac{b-a}{ab} \right)$
Or, $\dfrac{8h\left( ab \right)}{a-b}={{k}^{2}}$
Or ${{k}^{2}}=\dfrac{8ab}{b-a}.h$
Or ${{k}^{2}}=4\left( \dfrac{2ab}{b-a} \right).h$
Replacing $k$ by $y$and $h$ by $x$, we get:
${{y}^{2}}=4\left( \dfrac{2ab}{b-a} \right).x$
which clearly represents a parabola.
Hence, the locus of the midpoint of $PP'$ is the parabola ${{y}^{2}}=4\left( \dfrac{2ab}{b-a} \right).x$.
Now, in case if the latera recta of the parabolas are equal then:
We know, length of latus rectum of parabola ${{y}^{2}}=4ax$ is $4a$ and the length of latus rectum of parabola ${{y}^{2}}=-4bx$ is $4b$.
If the latera recta are equal, then
$4a=4b$
$\Rightarrow a=b$
$\Rightarrow b-a=0$
Now, when we substitute $b-a=0$ in the equation of locus, we get
${{y}^{2}}=4\left( \dfrac{2ab}{0} \right).x$
$\Rightarrow {{y}^{2}}=\infty$ which is an invalid curve.
Hence, for the locus to exist, the latera recta of the two parabolas must be unequal.
So, the locus of $P{{P}^{'}}$is a parabola , given by ${{y}^{2}}=4\left( \dfrac{2ab}{b-a} \right).x$, which exists only when the latera recta of the given two parabolas are unequal.

Note: Remember that the midpoint of two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$is given as $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$. Students generally make a mistake of writing it as $\left( \dfrac{{{x}_{1}}-{{x}_{2}}}{2},\dfrac{{{y}_{1}}-{{y}_{2}}}{2} \right)$.