Question
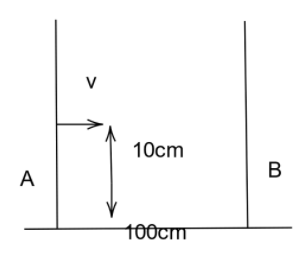
Question: Two paper screens \[A\] and \[B\] are separated by a distance of \[100m\] . A bullet pierces \[A\] a...
Two paper screens A and B are separated by a distance of 100m . A bullet pierces A and then B . The hole in B is 10cm below the hole in A . If the bullet is traveling horizontally at the time of hitting the screen A , calculate the velocity of the bullet when it hits the screen A . Neglect the resistance of paper and air.
Solution
We start by recording the given values and writing down the equations of motion. We find the value of time of motion and with the help of the value of time of motion, we use another equation of motion and find the value of the final velocity of the bullet.
Formulas used: Equation of motion, h=ut+21at2 and x=vt
Where, u is the initial velocity of the bullet (which is zero)
t is the time taken for the motion to happen
a is the acceleration related to the motion (here it is the acceleration due to gravity)
v is the final velocity of the bullet.
Complete step by step solution:
Let us start by gathering the given information
Distance between the screens,x=100cm
The distance between the holes in the screens, h=10cm
We use the equation of motion to find the time of this motion.
h=ut+21at2
The value of initial velocity is taken as zero and so the first term of the equation vanishes and we arrive at, h=21at2
We take the known values to one side and find the value of time of the motion using, t=a2h
Here, the value of acceleration will be equal to the value of acceleration due to gravity. We take 10 instead of 9.8 for easier calculation.t=102×0.10=0.14s
We have the value of time of the motion. Now we move onto find the final velocity, this can be found using another equation of motion
x=vt
Separating the known values to one side and substituting, we get v=tx=0.14100=707.11m/s
The final velocity of the motion will be 707.11m/s
Note:
Initial velocity is taken zero because the bullet is initially at rest. The conversion of centimeters to meters must be done or we will end up getting a different solution.
