Question

Two orthogonal circles are such that the area of one is twice the area of the other. If radius of smaller circle is r then diameter between the two centers is-
A.$\sqrt 3 r$
B.$2r$
C.$\sqrt 5 r$
D.$3r$

Answer 1

First use the formula of area of circle to find the area of both circles which is given as-
Area of the circle=$\pi {r^2}$ where r is the radius of the circle. Then find the value of another radius by solving them. Then use the condition of orthogonal circles which is-
$\Rightarrow r_1^2 + r_2^2 = {d^2}$ ---- (i)
Where ${r_1}$ is the radius of one circle while ${r_2}$ is the radius of the second circle and d is the diameter between the two centers of the two circles.

Complete step-by-step answer:
Given, two orthogonal circles are such that the area of one is twice the area of the other.
Also given the radius of the smaller circle is r.
We have to find the diameter between two centers.
We know that orthogonal circles are such circles which have tangent at their point of intersection at right angles. So if two circles are orthogonal then they must satisfy the following condition-

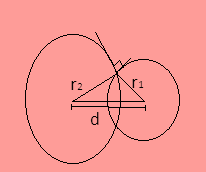
$\Rightarrow r_1^2 + r_2^2 = {d^2}$ ---- (i)
Where ${r_1}$ is the radius of one circle while ${r_2}$ is the radius of the second circle and d is the diameter between the two centers of the two circles.
Now we know that area of circle is given by the formula-
Area of the circle=$\pi {r^2}$ where r is the radius of the circle.
Now there are two circles smaller one with radius r and second with unknown radius.

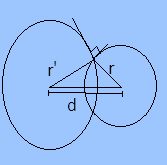
Let the radius of the second circle be r’. Then,
The area of smaller circle =$\pi {r^2}$
And the area of bigger circle =$\pi r{'^2}$
Now according to question-
$\Rightarrow \pi r{'^2} = 2\pi {r^2}$
On canceling the same terms we get,
$\Rightarrow r{'^2} = 2{r^2}$
On removing the square from both side we get,
$\Rightarrow r' = \sqrt 2 r$
Now if the two circles are orthogonal then,
$\Rightarrow r{'^2} + {r^2} = {d^2}$ [From condition (i)]
On putting the value of r’ we get,
$\Rightarrow 2{r^2} + {r^2} = {d^2}$
On adding we get,
$\Rightarrow 3{r^2} = {d^2}$
On taking square-root both side we get,
$\Rightarrow \sqrt 3 r = d$
Hence option A is the correct answer.

Note: Here the student may go wrong if they put $\pi {r^2} = 2\pi r{'^2}$ where r is the radius of the smaller circle. Since the circle which has radius r is smaller then, it is obvious that it will also have a smaller area as compared to the area of the bigger circle because the formula of area is given as $\pi {r^2}$ where r is the radius of the circle. And if $r < r'$ then $\pi {r^2} < \pi r{'^2}$. Hence we have written the statement of question as-
$\Rightarrow \pi r{'^2} = 2\pi {r^2}$