Question

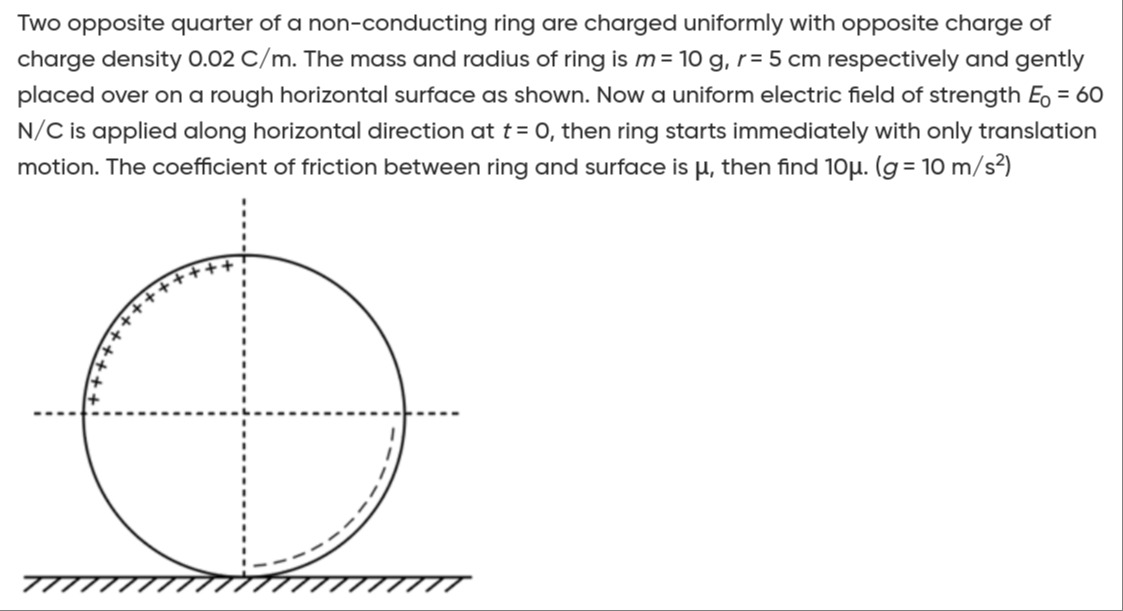
Two opposite quarter of a non-conducting ring are charged uniformly with opposite charge of charge density 0.02 C/m. The mass and radius of ring is $m = 10$ g, $r = 5$ cm respectively and gently placed over on a rough horizontal surface as shown. Now a uniform electric field of strength $E_0 = 60$ N/C is applied along horizontal direction at $t = 0$, then ring starts immediately with only translation motion. The coefficient of friction between ring and surface is $\mu$, then find $10\mu$. ($g = 10$ m/s²)

Answer 1

12

Answer 2

The problem describes a non-conducting ring with two opposite quarters charged uniformly with opposite charge density λ = 0.02 C/m. The radius of the ring is r = 5 cm = 0.05 m and its mass is m = 10 g = 0.01 kg. A uniform electric field E_0 = 60 N/C is applied horizontally. The ring starts with only translational motion, meaning its angular acceleration α = 0. We need to find 10μ, where μ is the coefficient of friction.

1. Calculate the charges on the quarters:

The length of a quarter ring is L = (1/4) * 2πr = πr/2.

Magnitude of charge on each quarter: |Q| = λL = λ(πr/2).

So, Q_+ = +λ(πr/2) and Q_- = -λ(πr/2).

2. Determine the net electric force on the ring:

Let the electric field E_0 be directed horizontally to the right (positive x-direction).

• Force on the positive quarter (Q_+) is F_+ = Q_+ E_0 to the right.
• Force on the negative quarter (Q_-) is F_- = Q_- E_0. Since Q_- is negative, F_- is directed to the left.

The net electric force F_E_net = F_+ + F_- = Q_+ E_0 + Q_- E_0 = (Q_+ + Q_-) E_0.

Since Q_+ = -Q_-, the total charge on the ring is Q_total = Q_+ + Q_- = 0.

Therefore, F_E_net = 0.

This implies that if the electric field is applied horizontally, there is no net horizontal force from the electric field, and thus no translational motion unless there's another force. However, the problem states "ring starts immediately with only translation motion". This means there must be a net horizontal force. The only way for this to happen with F_E_net = 0 is if the friction force provides the net force for translation.

3. Determine the net electric torque about the center of the ring:

For a uniformly charged quarter ring of radius r, the center of charge is located at (2r/π, 2r/π) relative to the center if it's in the first quadrant.

• For the positive quarter (top-left):

  The coordinates of its center of charge are (-2r/π, 2r/π).

  The force F_+ = Q_+ E_0 acts to the right.

  The torque due to F_+ about the center is τ_+ = (y-coordinate of CM) * F_+.

  τ_+ = (2r/π) * Q_+ E_0 = (2r/π) * (λπr/2) E_0 = λr^2 E_0.

  This torque is clockwise (positive y-lever arm with positive x-force).

• For the negative quarter (bottom-right):

  The coordinates of its center of charge are (2r/π, -2r/π).

  The force F_- = Q_- E_0. Since Q_- is negative, F_- is to the left (negative x-direction).

  The torque due to F_- about the center is τ_- = |y-coordinate of CM| * |F_-|.

  τ_- = |-2r/π| * |Q_-| E_0 = (2r/π) * (λπr/2) E_0 = λr^2 E_0.

  This torque is also clockwise (negative y-lever arm with negative x-force).

The total electric torque τ_E = τ_+ + τ_- = λr^2 E_0 + λr^2 E_0 = 2λr^2 E_0 (clockwise).

4. Apply the condition of "only translational motion":

This means the angular acceleration α = 0. Therefore, the net torque about the center of mass must be zero.

The electric torque τ_E is clockwise. To prevent rotation, the friction force f at the contact point must provide an equal and opposite (counter-clockwise) torque.

The point of contact is at the bottom of the ring. For a counter-clockwise torque, the friction force f must act to the right.

Torque due to friction τ_f = f * r.

So, τ_E = τ_f

2λr^2 E_0 = f * r

f = 2λrE_0.

5. Apply Newton's second law for translational motion:

The horizontal forces acting on the ring are the net electric force F_E_net and the friction force f.

Since F_E_net = 0, the net force for translational motion is entirely due to friction.

F_net = ma

f = ma

Substituting f = 2λrE_0:

2λrE_0 = ma.

This equation gives the acceleration a of the ring.

6. Determine the coefficient of friction μ:

Since the ring is sliding (only translational motion, no rotation), the friction force is kinetic friction: f = μN.

On a horizontal surface, the normal force N = mg.

So, f = μmg.

Equating the two expressions for friction:

μmg = 2λrE_0

μ = (2λrE_0) / (mg)

7. Substitute the given values:

λ = 0.02 C/m

r = 0.05 m

E_0 = 60 N/C

m = 0.01 kg

g = 10 m/s²

μ = (2 * 0.02 * 0.05 * 60) / (0.01 * 10)

μ = (0.04 * 0.05 * 60) / 0.1

μ = (0.002 * 60) / 0.1

μ = 0.12 / 0.1

μ = 1.2

8. Calculate the requested value:

The question asks for 10μ.

10μ = 10 * 1.2 = 12.