Question

Two of the normals drawn from a point $O$ to the curve make complementary angles with the axis; prove that the locus of $O$ and the curve which is touched by its polar are parabolas such that their latera recta and that of the original parabola form a geometrical progression. Sketch the three curves.

Answer 1

Hint: Use the results that for a co normal point, three normal of slopes $m1$, $m2$and $m3$ satisfy $m1+m2+m3=0,\,m1m2+m2m3+m1m3=\dfrac{2a-h}{a}\,and\,m1m2m3=-\dfrac{k}{a}$ to find the locus of $O$, or the second parabola. Then make use of the concept of pole and polar, with $O$ as the pole, and then make the polar satisfy the general equation of tangent which is $y=mx+\dfrac{a}{m}$ to arrive at the third and final parabola.

Complete step-by-step answer:
Let the parabola to be considered in this question have the equation ${{y}^{2}}=4ax$. A parabola with this general form has the $x$ axis as its axis and its vertex lies at the origin. The focus of this parabola is located at a point $(a,0)$, lying on the $x$ axis, and the length of its latus rectum = $4a$.
The first part of the question asks us to find the locus of a point $O$, from where two normal drops to the parabola always make complementary angles with the $x$ axis. This means that the sum of both the angles will be equal to ${{90}^{\circ }}$.
The general equation of any normal dropped to a parabola is :
$y=mx-2am-a{{m}^{3}}$. This normal passes through the point $(a{{m}^{2}},-2am)$ on the parabola, and through the point from which it was dropped. Let’s call that point $O$, and let its coordinates be $(h,k)$, since this is the point we need to find the locus of.
Whenever there are three normal drops on a parabola, from the same point, the feet of those three normals are called co normal points, i.e. the three points where the respective normals cut the parabola, are called co normal points.
Here’s a drawing of the point $O$ on the main parabola, but for ease of drawing we take a particular case, where $a=1$.

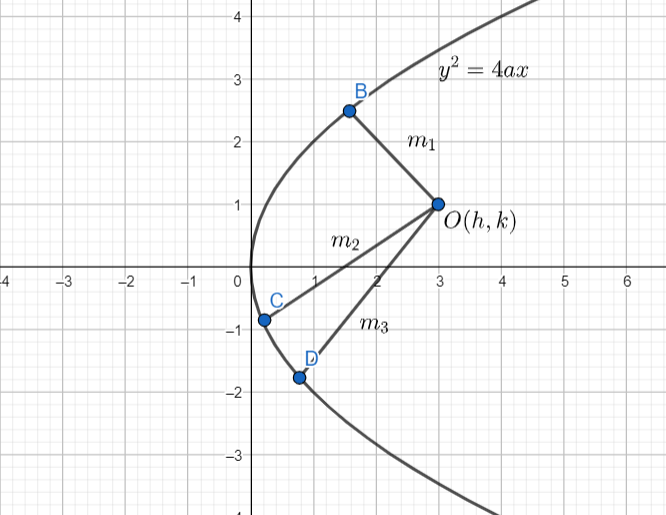
The general equation of a normal to the parabola is : $y=mx-2am-a{{m}^{3}}$, as mentioned before.
Let’s make the poinht $O$ $(h,k)$ satisfy our general equation, since the normals we’re talking about have to pass through $O$.
Substituting $x=h$ and $y=k$ in the general equation, we get :
$\begin{aligned} & y=mx-2am-a{{m}^{3}} \\\ & \Rightarrow k=mh-2am-a{{m}^{3}} \\\ & \Rightarrow a{{m}^{3}}+2am-mh+k=0 \\\ & \Rightarrow a{{m}^{3}}+m(2a-h)+k=0 \\\ \end{aligned}$ ………………….(1)
For $O$ to be point satisfying the general equation of a normal, we got a cubic equation in terms of $m$. Thus, the cubic tells us that there can be three values of $m$, or there can be three different normals dropped to the parabola, all of which pass through $O$, and have different slopes. The slopes are what we get from (1)’s roots.
For a cubic equation, sum of roots = $-\dfrac{b}{a}$
Product of roots taken two at a time = $\dfrac{c}{a}$
And, product of all the roots = $-\dfrac{d}{a}$
For equation (1), $a=a,b=0,c=2a-h,d=k$ since the general form of a cubic equation used for deriving the above results is : $a{{x}^{3}}+b{{x}^{2}}+cx+d=0$, where $x$ is the variable, here, replaced by $m$.
Let’s call the three different roots obtained from (1) ${{m}_{1}},{{m}_{2}},{{m}_{3}}$.
Therefore, they should satisfy the conditions mentioned above.
$\begin{aligned} & {{m}_{1}}+{{m}_{2}}+{{m}_{3}}=-\dfrac{b}{a} \\\ & \Rightarrow {{m}_{1}}+{{m}_{2}}+{{m}_{3}}=0 \\\ \end{aligned}$…………………..(2) satisfies the first condition.
$\begin{aligned} & {{m}_{1}}{{m}_{2}}+{{m}_{2}}{{m}_{3}}+{{m}_{3}}{{m}_{1}}=\dfrac{c}{a} \\\ & \Rightarrow {{m}_{1}}{{m}_{2}}+{{m}_{2}}{{m}_{3}}+{{m}_{3}}{{m}_{1}}=\dfrac{2a-h}{a} \\\ \end{aligned}$ ………………..(3) satisfies the second condition
$\begin{aligned} & {{m}_{1}}{{m}_{2}}{{m}_{3}}=-\dfrac{d}{a} \\\ & \Rightarrow {{m}_{1}}{{m}_{2}}{{m}_{3}}=-\dfrac{k}{a} \\\ \end{aligned}$ ……………………(4) satisfies the third condition.
Let the tangents that make complementary angles have their slopes = ${{m}_{1}}$ and ${{m}_{2}}$.
Since we know that for any line, $m=\tan \alpha$, if the line makes an angle $\alpha$with the positive $x$ axis, let’s say that ${{m}_{1}}=\tan \alpha$ and ${{m}_{2}}=\tan \beta$.
If the angles $\alpha$ and $\beta$ are complementary, it means that $\alpha +\beta ={{90}^{\circ }}$.
Applying formula $\tan (\alpha +\beta )=\dfrac{\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }$,
We’ll have : $\tan {{90}^{\circ }}=\dfrac{{{m}_{1}}+{{m}_{2}}}{1-{{m}_{1}}{{m}_{2}}}$
We know that $\tan {{90}^{\circ }}=\infty$, and for this the denominator has to be 0.
Therefore, $\Rightarrow 1-{{m}_{1}}{{m}_{2}}=0$
$\Rightarrow {{m}_{1}}{{m}_{2}}=1$ ……………………(5)
Simplifying (2), we get :
${{m}_{1}}+{{m}_{2}}+{{m}_{3}}=0$
$\Rightarrow {{m}_{1}}+{{m}_{2}}=-{{m}_{3}}$
$\Rightarrow {{m}_{3}}=-({{m}_{1}}+{{m}_{2}})$
Simplifying (3), we get :
${{m}_{1}}{{m}_{2}}{{m}_{3}}=-\dfrac{k}{a}$
$\Rightarrow {{m}_{3}}=-\dfrac{k}{a({{m}_{1}}{{m}_{2}})}$
$\Rightarrow {{m}_{3}}=-\dfrac{k}{a}$
Simplifying (2), we get :
${{m}_{1}}{{m}_{2}}+{{m}_{2}}{{m}_{3}}+{{m}_{3}}{{m}_{1}}=\dfrac{2a-h}{a}$
$\Rightarrow 1+{{m}_{3}}({{m}_{1}}+{{m}_{2}})=\dfrac{2a-h}{a}$
$\Rightarrow 1+{{m}_{3}}(-{{m}_{3}})=\dfrac{2a-h}{a}$
$\Rightarrow 1-{{({{m}_{3}})}^{2}}=\dfrac{2a-h}{a}$
$\Rightarrow 1-{{\left( -\dfrac{k}{a} \right)}^{2}}=\dfrac{2a-h}{a}$
$\Rightarrow 1-\dfrac{{{k}^{2}}}{{{a}^{2}}}=\dfrac{2a-h}{a}$
$\Rightarrow \dfrac{{{a}^{2}}-{{k}^{2}}}{{{a}^{2}}}=\dfrac{2a-h}{a}$
$\Rightarrow {{a}^{2}}-{{k}^{2}}=a(2a-h)$
$\Rightarrow {{a}^{2}}-{{k}^{2}}=2{{a}^{2}}-ah$
$\Rightarrow {{k}^{2}}=ah-{{a}^{2}}$
$\Rightarrow {{k}^{2}}=a(h-a)$
Since we had to find the locus of the point $O$ $(h,k)$ , we replace $(h,k)$ with $(x,y)$. Replacing, we get :
$\Rightarrow {{y}^{2}}=a(x-a)$ …………………(6)
Comparing equation (6), with the general equation of a parabola we get to know that :
This equation represents the equation of a parabola, with its axis on the $x$ axis, and its vertex at $(a,0)$. The focus of this parabola would be $\left( a+\dfrac{a}{4},0 \right)=\left( \dfrac{5a}{4},0 \right)$.
The next part of the question asks us to find the polar of the point $O$. The coordinates of the point $O$ we decided were $(h,k)$. To find the polar of a point, we’ll use the formula that says :
The polar of a point $(x,y)$ : $Dx+Ey+F=0$, where $2D=$coefficient of $2x$ in the original equation, $E$ = $y$ coordinate of pole (here, point $O$) and $F=2a$ multiplied by the $x$ coordinate of the pole (here, point $O$).
Substituting, we get :
$2D=4a$
$\Rightarrow D=2a$ ,
$E=k$ and
$F=2ah$
Substituting all these values in the equation $Dx+Ey+F=0$, we get :
$2ax+ky+2ah=0$
$\Rightarrow ky=-2ax-2ah$
$\Rightarrow ky=-2a(x+h)$ ……………………(7)
We now need to find the parabola that line (7) acts as the tangent to.
The easiest way to do this would be to compare (7) with the general equation of a tangent to a parabola ${{y}^{2}}=4Ax$. The general equation of a tangent of slope $m$ would be : $y=mx+\dfrac{A}{m}$.
Let’s try and reshape (7) to make it look similar to the general equation of a tangent just mentioned.
Rearranging (7), we get :
$\begin{aligned} & ky=-2a(x+h) \\\ & \Rightarrow y=-\dfrac{2a}{k}(x+h) \\\ & \Rightarrow y=-\dfrac{2ax}{k}-\dfrac{2ah}{k} \\\ & \Rightarrow y=\left( -\dfrac{2a}{k} \right)x-\dfrac{2({{k}^{2}}+{{a}^{2}})}{k} \\\ & \Rightarrow y=-\dfrac{2ax}{k}-\dfrac{2{{a}^{2}}}{k}-2k \\\ & \Rightarrow y=\left( -\dfrac{2a}{k} \right)(x+a)+\dfrac{4a}{\left( -\dfrac{2a}{k} \right)} \\\ \end{aligned}$
The final equation that we have here can now be compared to the general equation of a tangent to a parabola. After comparing, we can clearly see that :
$m=-\dfrac{2a}{k}$ and for the new parabola (let’s call it ${{y}^{2}}=4Ax$ itself),
$A=4a$
Therefore, the curve which is touched by the polar to point $O$ has the equation:
$\begin{aligned} & {{y}^{2}}=4Ax \\\ & \Rightarrow {{y}^{2}}=4(4a)x \\\ & \Rightarrow {{y}^{2}}=16ax \\\ \end{aligned}$
Thus, we finally have three parabolas.
The first one is the original parabola : ${{y}^{2}}=4ax$
The second one is the locus of point $O$ : ${{y}^{2}}=a(x-a)$
The third one is the curve to which the polar of point $O$ is a tangent : ${{y}^{2}}=16ax$
The length of the latus rectum of any parabola = the coefficient of $x$ in the equation.
For the first parabola, length of latus rectum = 4a
For the second parabola, we need to shift the origin to the point $(a,0)$ so that we can better compare it with the general form.
To shift origin, we define new variables : $X=x-a$ and $Y=y$.
Substituting for these variables, we get : ${{Y}^{2}}=aX$
Thus, the length of the latus rectum of the second parabola = coefficient of $X=a$
The length of latus rectum of third equation = coefficient of $x=16a$ .
Now, we can clearly see, that, $a,4a,16a$ are in geometric progression since
$\dfrac{16a}{4a}=\dfrac{4a}{a}=4$= common ratio of the GP.
Hence proved.
Hence proved that the three curves’ latus recta are in GP.

Note: You should also note that just because it is said that the angle made by the normals are complementary, it doesn’t mean that the two normals are perpendicular to each other. Approaching the method where the product of their slopes will be $=-1$ will make you reach the wrong answer.