Solveeit Logo
Login

Question

Question: Two objects A and B are moving along the directions as shown in the figure. Find the magnitude and d...

Two objects A and B are moving along the directions as shown in the figure. Find the magnitude and direction of the relative velocity of B w.r.t. A.

Explanation

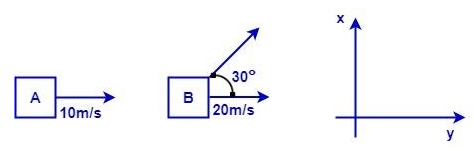
Solution

Hint Relative velocity of B w.r.t. A is given by:
⇒vBA→=vB→−vA→\Rightarrow \overrightarrow{{{v}_{BA}}}=\overrightarrow{{{v}_{B}}}-\overrightarrow{{{v}_{A}}}
Magnitude of this relative velocity is ∣vBA→∣\left| \overrightarrow{{{v}_{BA}}} \right|
Direction of this relative velocity is given by the angle α\alpha which is calculated by:
⇒tan⁡α=vBAyvBAx\Rightarrow \tan \alpha =\frac{{{v}_{B{{A}_{y}}}}}{{{v}_{B{{A}_{x}}}}}
Where vBAy{{v}_{B{{A}_{y}}}} and vBAx{{v}_{B{{A}_{x}}}} are the y and x components of vBA→\overrightarrow{{{v}_{BA}}} .

Complete step by step solution
⇒vA→=10i^ ⇒Here taking the components of velocity of B; ⇒vB→=20cos⁡30∘i^+20sin⁡30∘j^ ⇒103i^+10j^ \begin{aligned} &\Rightarrow \overrightarrow{{{v}_{A}}}=10\widehat{i} \\\ &\Rightarrow \text{Here taking the components of velocity of B;} \\\ &\Rightarrow \overrightarrow{{{v}_{B}}}=20\cos 30{}^\circ \widehat{i}+20\sin 30{}^\circ \widehat{j} \\\ &\Rightarrow10\sqrt{3}\widehat{i}+10\widehat{j} \\\ \end{aligned}
Relative velocity of B w.r.t. A is
⇒vBA→=vB→−vA→ ⇒=103i^+10j^−103i^ ⇒=10(3−1)i^+10j^ \begin{aligned} &\Rightarrow \overrightarrow{{{v}_{BA}}}=\overrightarrow{{{v}_{B}}}-\overrightarrow{{{v}_{A}}} \\\ &\Rightarrow =10\sqrt{3}\widehat{i}+10\widehat{j}-10\sqrt{3}\widehat{i} \\\ &\Rightarrow =10\left( \sqrt{3}-1 \right)\widehat{i}+10\widehat{j} \\\ \end{aligned}
Now ⇒∣vBA→∣=10(3−1)2+12 ⇒103+1−23+1 ⇒∣vBA→∣=105−23ms−1 For direction; ⇒tan⁡α=1010(3−1) ⇒tan⁡α=13−1 ⇒α=tan⁡−1(13−1) \begin{aligned} & Now \\\ &\Rightarrow \left| \overrightarrow{{{v}_{BA}}} \right|=10\sqrt{{{\left( \sqrt{3}-1 \right)}^{2}}+{{1}^{2}}} \\\ &\Rightarrow10\sqrt{3+1-2\sqrt{3}+1} \\\ &\Rightarrow \left| \overrightarrow{{{v}_{BA}}} \right|=10\sqrt{5-2\sqrt{3}}m{{s}^{-1}} \\\ & \text{For direction;} \\\ &\Rightarrow \tan \alpha =\frac{10}{10\left( \sqrt{3}-1 \right)} \\\ &\Rightarrow \tan \alpha =\frac{1}{\sqrt{3}-1} \\\ &\Rightarrow \alpha ={{\tan }^{-1}}\left( \frac{1}{\sqrt{3}-1} \right) \\\ \end{aligned} .

Note
Alternate method:
Velocity of B w.r.t. A:
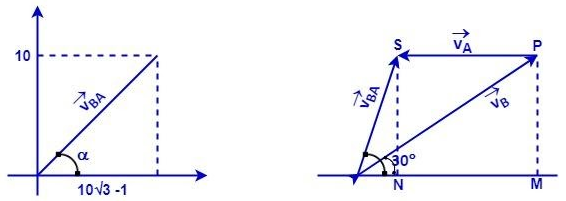
⇒vBA→=vB→+(−vA→)\Rightarrow \overrightarrow{{{v}_{BA}}}=\overrightarrow{{{v}_{B}}}+\left( -\overrightarrow{{{v}_{A}}} \right)

From the figure;
⇒NS=MP=20sin⁡30∘ ⇒NS=10 and ⇒ON=OM−NM ⇒ON=20cos⁡30∘−10 ⇒ON=10(3−1) ⇒∣vBA→∣=ON2+NS2 ⇒∣vBA→∣=10(3−1)2+12 ⇒∣vBA→∣=105−23ms−1 \begin{aligned} &\Rightarrow NS=MP=20\sin 30{}^\circ \\\ &\Rightarrow NS=10 \\\ & and \\\ &\Rightarrow ON=OM-NM \\\ &\Rightarrow ON=20\cos 30{}^\circ -10 \\\ &\Rightarrow ON=10\left( \sqrt{3}-1 \right) \\\ &\Rightarrow \left| \overrightarrow{{{v}_{BA}}} \right|=\sqrt{O{{N}^{2}}+N{{S}^{2}}} \\\ &\Rightarrow \left| \overrightarrow{{{v}_{BA}}} \right|=10\sqrt{{{\left( \sqrt{3}-1 \right)}^{2}}+{{1}^{2}}} \\\ &\Rightarrow \left| \overrightarrow{{{v}_{BA}}} \right|=10\sqrt{5-2\sqrt{3}}m{{s}^{-1}} \\\ \end{aligned}
For direction; ⇒tan α=NSON ⇒tan⁡α=1010(3−1) ⇒tan⁡α=13−1 ⇒α=tan⁡−1(13−1) \begin{aligned} & \text{For direction;} \\\ &\Rightarrow \text{tan }\alpha =\frac{NS}{ON} \\\ &\Rightarrow \tan \alpha =\frac{10}{10\left( \sqrt{3}-1 \right)} \\\ &\Rightarrow \tan \alpha =\frac{1}{\sqrt{3}-1} \\\ &\Rightarrow \alpha ={{\tan }^{-1}}\left( \frac{1}{\sqrt{3}-1} \right) \\\ \end{aligned} .