Question

Two numbers are selected independently at random in the interval $[0, 1]$. If the smaller one is less than $1/3$, then find the probability that the larger one is greater than $3/4$.

Answer 1

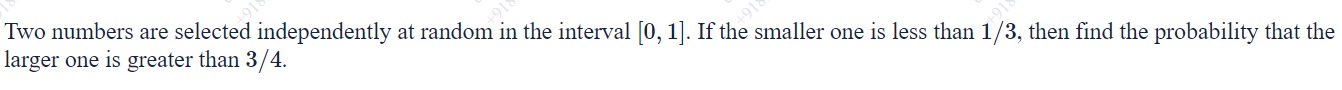
3/10

Answer 2

Let $X$ and $Y$ be the two numbers selected independently at random from the interval $[0, 1]$. The sample space is the unit square $[0, 1] \times [0, 1]$ with area 1. The probability of any event is the area of the corresponding region in the unit square.

Let $U = \min(X, Y)$ and $V = \max(X, Y)$. We are given the event $B: U < 1/3$. We want to find the probability of the event $A: V > 3/4$, given $B$. This is $P(A \mid B) = \frac{P(A \cap B)}{P(B)}$.

First, let's find $P(B) = P(\min(X, Y) < 1/3)$. The complementary event is $B^c: \min(X, Y) \ge 1/3$. This means $X \ge 1/3$ and $Y \ge 1/3$. The region for $B^c$ is the square $[1/3, 1] \times [1/3, 1]$. The side length of this square is $1 - 1/3 = 2/3$. The area of this square is $(2/3)^2 = 4/9$. So, $P(B^c) = 4/9$. $P(B) = P(\min(X, Y) < 1/3) = 1 - P(B^c) = 1 - 4/9 = 5/9$.

Next, let's find $P(A \cap B) = P(\max(X, Y) > 3/4 \text{ and } \min(X, Y) < 1/3)$. The condition $\max(X, Y) > 3/4$ means $X > 3/4$ or $Y > 3/4$. The condition $\min(X, Y) < 1/3$ means $X < 1/3$ or $Y < 1/3$.

We are looking for the area of the region where $(X > 3/4 \text{ or } Y > 3/4)$ AND $(X < 1/3 \text{ or } Y < 1/3)$. Let's analyze the four possible combinations of the conditions:

1. ($X > 3/4$) AND ($X < 1/3$): This is impossible since $1/3 < 3/4$.
2. ($X > 3/4$) AND ($Y < 1/3$): This region is the rectangle $(3/4, 1] \times [0, 1/3)$. The area is $(1 - 3/4) \times (1/3 - 0) = (1/4) \times (1/3) = 1/12$. For any point $(X, Y)$ in this region, $X > 3/4$ and $Y < 1/3$. Since $3/4 > 1/3$, we have $X > Y$. So $\max(X, Y) = X > 3/4$ and $\min(X, Y) = Y < 1/3$. This region satisfies both conditions.
3. ($Y > 3/4$) AND ($X < 1/3$): This region is the rectangle $[0, 1/3) \times (3/4, 1]$. The area is $(1/3 - 0) \times (1 - 3/4) = (1/3) \times (1/4) = 1/12$. For any point $(X, Y)$ in this region, $X < 1/3$ and $Y > 3/4$. Since $1/3 < 3/4$, we have $X < Y$. So $\max(X, Y) = Y > 3/4$ and $\min(X, Y) = X < 1/3$. This region satisfies both conditions.
4. ($Y > 3/4$) AND ($Y < 1/3$): This is impossible since $1/3 < 3/4$.

The region for $(A \cap B)$ is the union of the two disjoint rectangles from combinations 2 and 3: $R_1 = \{(X, Y) \mid 3/4 < X \le 1, 0 \le Y < 1/3 \}$ $R_2 = \{(X, Y) \mid 0 \le X < 1/3, 3/4 < Y \le 1 \}$ The total area of this region is Area($R_1$) + Area($R_2$) = $1/12 + 1/12 = 2/12 = 1/6$. So, $P(A \cap B) = 1/6$.

Finally, the conditional probability is $P(A \mid B) = \frac{P(A \cap B)}{P(B)} = \frac{1/6}{5/9}$. $P(A \mid B) = \frac{1}{6} \times \frac{9}{5} = \frac{9}{30} = \frac{3}{10}$.

The final answer is $\frac{3}{10}$.

In summary:

• $P(B) = 5/9$
• $P(A \cap B) = 1/6$
• $P(A \mid B) = \frac{1/6}{5/9} = \frac{3}{10}$