Question

Two normal fair dice are rolled. Let A be the event that the sum of the points on the faces shown is odd & B the event that atleast one face shows up 3. The probability of the event P(AUB) =

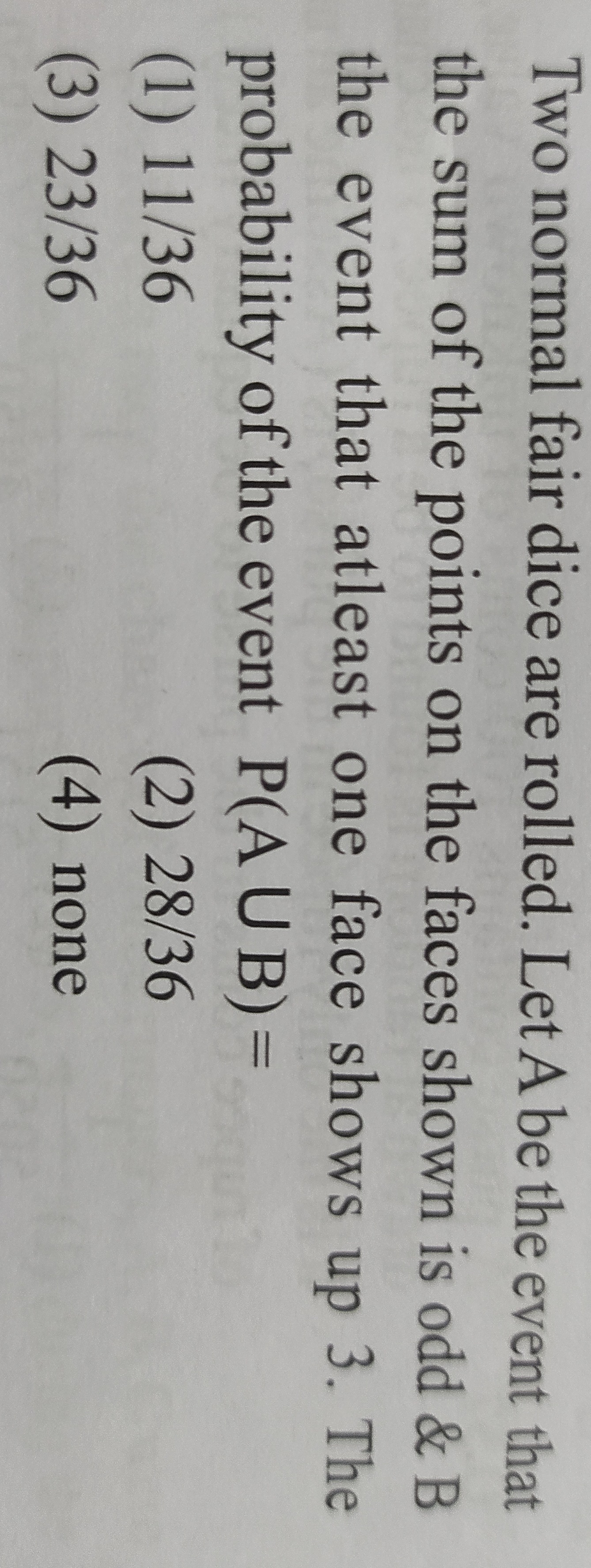
• A. 11/36
• B. 28/36
• C. 23/36
• D. none

Answer 1

Answer: (C)

23/36

Answer 2

The sample space $\Omega$ when rolling two normal fair dice consists of $6 \times 6 = 36$ possible outcomes, each equally likely. Each outcome is an ordered pair $(d_1, d_2)$, where $d_1$ is the result of the first die and $d_2$ is the result of the second die.

Let A be the event that the sum of the points on the faces shown is odd. The sum $d_1 + d_2$ is odd if and only if one die shows an odd number and the other shows an even number.
There are 3 odd numbers (1, 3, 5) and 3 even numbers (2, 4, 6) on a die.
The number of outcomes where $d_1$ is odd and $d_2$ is even is $3 \times 3 = 9$.
The number of outcomes where $d_1$ is even and $d_2$ is odd is $3 \times 3 = 9$.
So, the total number of outcomes in event A is $|A| = 9 + 9 = 18$.
The probability of event A is $P(A) = \frac{|A|}{|\Omega|} = \frac{18}{36} = \frac{1}{2}$.

Let B be the event that at least one face shows up 3. This means either the first die is 3, or the second die is 3, or both are 3.
Outcomes where the first die is 3: (3,1), (3,2), (3,3), (3,4), (3,5), (3,6) (6 outcomes).
Outcomes where the second die is 3: (1,3), (2,3), (3,3), (4,3), (5,3), (6,3) (6 outcomes).
The outcome (3,3) is in both sets, so we count it once.
The number of outcomes in event B is $|B| = 6 + 6 - 1 = 11$.
The outcomes in B are: (3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (1,3), (2,3), (4,3), (5,3), (6,3).
The probability of event B is $P(B) = \frac{|B|}{|\Omega|} = \frac{11}{36}$.

We want to find the probability of the event $A \cup B$, which is $P(A \cup B)$.
Using the formula $P(A \cup B) = P(A) + P(B) - P(A \cap B)$.
We need to find the probability of the intersection of events A and B, $P(A \cap B)$.
Event $A \cap B$ is the event that the sum is odd AND at least one face shows up 3.
We look at the outcomes in B and check which ones have an odd sum:
(3,1): Sum = 4 (even) - Not in A
(3,2): Sum = 5 (odd) - In A
(3,3): Sum = 6 (even) - Not in A
(3,4): Sum = 7 (odd) - In A
(3,5): Sum = 8 (even) - Not in A
(3,6): Sum = 9 (odd) - In A
(1,3): Sum = 4 (even) - Not in A
(2,3): Sum = 5 (odd) - In A
(4,3): Sum = 7 (odd) - In A
(5,3): Sum = 8 (even) - Not in A
(6,3): Sum = 9 (odd) - In A
The outcomes in $A \cap B$ are: (3,2), (3,4), (3,6), (2,3), (4,3), (6,3).
The number of outcomes in $A \cap B$ is $|A \cap B| = 6$.
The probability of event $A \cap B$ is $P(A \cap B) = \frac{|A \cap B|}{|\Omega|} = \frac{6}{36}$.

Now we can calculate $P(A \cup B)$:
$P(A \cup B) = P(A) + P(B) - P(A \cap B)$
$P(A \cup B) = \frac{18}{36} + \frac{11}{36} - \frac{6}{36}$
$P(A \cup B) = \frac{18 + 11 - 6}{36}$
$P(A \cup B) = \frac{29 - 6}{36}$
$P(A \cup B) = \frac{23}{36}$.

Alternatively, we can find the number of outcomes in $A \cup B$ directly.
$|A \cup B| = |A| + |B| - |A \cap B| = 18 + 11 - 6 = 23$.
The probability $P(A \cup B) = \frac{|A \cup B|}{|\Omega|} = \frac{23}{36}$.