Question

Two non-conducting solid spheres of radii R and 2R, having uniform volume charge densities ${{\rho }_{1}}$ and ${{\rho }_{2}}$ respectively, touch each other. The net electric field at a distance 2R from the centre of the smaller sphere, along the line joining the centre of the spheres is zero. The ratio $\dfrac{{{\rho }_{1}}}{{{\rho }_{2}}}$ can be:
(This question has multiple correct options)
$\text{A}\text{. }-4$
$\text{B}\text{. }-\dfrac{32}{25}$
$\text{C}\text{. }\dfrac{32}{25}$
$\text{D}\text{. 4}$

Answer 1

To solve this problem one needs the formula for the electric field due to a charged non conducting sphere at a point outside the sphere. And also the formula for electric field at a point inside the non conducting sphere due to its own charge. Use these formulae and equate the net force to zero.
Formula used:
$E=\dfrac{KQ}{{{r}^{2}}}$
$E=\dfrac{KQr}{{{R}^{3}}}$
$\rho =\dfrac{Q}{\dfrac{4}{3}\pi {{R}^{3}}}$

Complete answer:
First draw a figure for the given data as shown below.

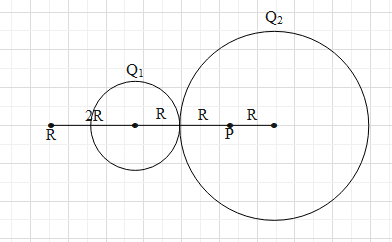
The electric field due to a charged non-conducting sphere at a point is given as $E=\dfrac{KQ}{{{r}^{2}}}$, where Q is the charge in the sphere, K is a proportionality constant and r is the distance of the point from the centre of the sphere. The direction of the field is radially outwards for positive charge.
If the point is inside the sphere at distance r, such hat r < R (radius of the sphere), then the electric field at this point is given as $E=\dfrac{KQr}{{{R}^{3}}}$. The direction of the field is radially outwards for positive charge.
Let the charge on the smaller and larger sphere is ${{Q}_{1}}$ and ${{Q}_{2}}$ respectively.
$\Rightarrow {{\rho }_{1}}=\dfrac{{{Q}_{1}}}{\dfrac{4}{3}\pi {{R}^{3}}}$
$\Rightarrow {{Q}_{1}}=\dfrac{4}{3}\pi {{R}^{3}}{{\rho }_{1}}$…. (i).
And
$\Rightarrow {{\rho }_{2}}=\dfrac{{{Q}_{2}}}{\dfrac{4}{3}\pi {{(2R)}^{3}}}=\dfrac{{{Q}_{2}}}{\dfrac{32}{3}\pi {{R}^{3}}}$
$\Rightarrow {{Q}_{2}}=\dfrac{32}{3}\pi {{R}^{3}}{{\rho }_{2}}$ …. (ii)
There are points at a distance of 2R from the centre of the smaller sphere, P and R.
The point P is out the smaller sphere at distance of 2R from its centre. Therefore, the electric field due to this sphere at P is ${{E}_{1}}=\dfrac{K{{Q}_{1}}}{{{(2R)}^{2}}}=\dfrac{K{{Q}_{1}}}{4{{R}^{2}}}$.
The direction of ${{E}_{1}}$ is towards the right.
The given point is inside the bigger sphere at distance of R from its centre. Therefore, the electric field due to this sphere at P is ${{E}_{2}}=\dfrac{K{{Q}_{2}}R}{{{(2R)}^{3}}}=\dfrac{K{{Q}_{2}}}{8{{R}^{2}}}$.
The direction of ${{E}_{2}}$ is towards the left.
Therefore, the net electric field at P is $E={{E}_{1}}-{{E}_{2}}$
$\Rightarrow E=\dfrac{K{{Q}_{1}}}{4{{R}^{2}}}-\dfrac{K{{Q}_{2}}}{8{{R}^{2}}}$.
But it is said that the electric field at P is zero.
$\Rightarrow E=\dfrac{K{{Q}_{1}}}{4{{R}^{2}}}-\dfrac{K{{Q}_{2}}}{8{{R}^{2}}}=0$
$\Rightarrow \dfrac{K{{Q}_{1}}}{4{{R}^{2}}}=\dfrac{K{{Q}_{2}}}{8{{R}^{2}}}$
$\Rightarrow 2{{Q}_{1}}={{Q}_{2}}$
Substitute the values of ${{Q}_{1}}$ and ${{Q}_{2}}$ from (i) and (ii).
$\Rightarrow 2\left( \dfrac{4}{3}\pi {{R}^{3}}{{\rho }_{1}} \right)=\dfrac{32}{3}\pi {{R}^{3}}{{\rho }_{2}}$
$\Rightarrow {{\rho }_{1}}=4{{\rho }_{2}}$
$\Rightarrow \dfrac{{{\rho }_{1}}}{{{\rho }_{2}}}=4$
Point R is outside both the spheres. It is at distance of 5R from the centre of the bigger to its left and 2R to the left of centre of the smaller sphere.
However, in this case one of the spheres must be negatively charged so that the two electric fields at R point in opposite directions.
Let the smaller sphere be negatively charged. Therefore, at R, ${{E}_{1}}$ will be directed towards right and ${{E}_{2}}$ will be directed towards left.
Now, by the same procedure as above, we get the net electric at R as $E={{E}_{1}}-{{E}_{2}}=\dfrac{K{{Q}_{1}}}{4{{R}^{2}}}-\dfrac{K{{Q}_{2}}}{25{{R}^{2}}}=0$
$\Rightarrow \dfrac{K{{Q}_{1}}}{4{{R}^{2}}}=\dfrac{K{{Q}_{2}}}{25{{R}^{2}}}$
$\Rightarrow 25{{Q}_{1}}=4{{Q}_{2}}$
$\Rightarrow 25\left( \dfrac{4}{3}\pi {{R}^{3}}{{\rho }_{1}} \right)=4\left( \dfrac{32}{3}\pi {{R}^{3}}{{\rho }_{2}} \right)$
$\Rightarrow 25{{\rho }_{1}}=32{{\rho }_{2}}$
$\Rightarrow \dfrac{{{\rho }_{1}}}{{{\rho }_{2}}}=\dfrac{32}{25}$.
But since one sphere has a positive charge density and other has a negative charge density,
$\Rightarrow \dfrac{{{\rho }_{1}}}{{{\rho }_{2}}}=-\dfrac{32}{25}$.

So, the correct answer is “Option B and D”.

Note:
The statement saying that the two given spheres are non conducting is very important in this question. It is because the two spheres are non conducting, the two do not interact with each when they are in contact.
If the sphere were conductors, then there will be transfer of charges from a sphere at higher potential to a sphere at lower potential until both attain equal potential, when they are connected