Solveeit Logo
Login

Question

Question: Two moles of helium gas undergo a cyclic process as shown in figure. Assuming the gas to be ideal. T...

Two moles of helium gas undergo a cyclic process as shown in figure. Assuming the gas to be ideal. The net work done by the gas is
A. 200R  I⁡n2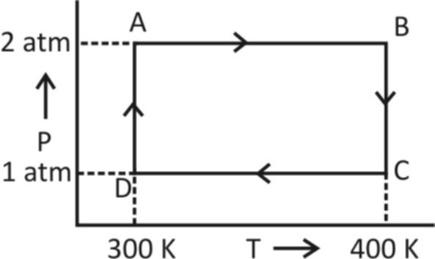200R\,\,\operatorname{I} n2
B. 100R  I⁡n2100R\,\,\operatorname{I} n2
C. 300R  I⁡n2300R\,\,\operatorname{I} n2
D. 400R  I⁡n2400R\,\,\operatorname{I} n2

Explanation

Solution

Concept of work done in case of isothermal process and isobaric process. As the processes AB and CD occur at constant pressure so it is barbaric while processes BC and DA occur at constant temperature so isothermal

Formula used:
1. Work done in an isobaric process
W=PΔV=nRΔTW = P\Delta V = nR\Delta T
2. Work done in an isothermal process
=nRT  ℓn  P1P2= nRT\,\,\ell n\,\dfrac{{\,{P_1}}}{{{P_2}}}

Complete step by step answer:
1. Isobaric Process – A process which occurs under constant pressure is called isobaric process.
2. Isothermal Process- A process which occurs for the same temperature is called isotherm process.
3. Isochoric Process- A process for which volume remains constant is called isochoric process.
4. Adiabatic Process- A process which involves no exchange of heat is called adiabatic from now, from the given figure, it is clear that both AB and CD processes involve no change in pressure. So, AB and CD represent isobaric processes.
Work done == PΔV=nRΔTP\Delta V = nR\Delta T
Where is pressure, R is gas constant, n is number of moles, Δ→\Delta \to change, V is volume, T is temperature.
Now, work done for AB is given by
WAB=nR(T2−T1){W_{AB}} = nR\left( {{T_2} - {T_1}} \right)
  ⟹  WAB=nR(400−300)    [asT1=300K, T2=400K]\implies {W_{AB}} = nR\left( {400 - 300} \right)\,\,\,\,\left[ {as{T_1} = 300K,\,{T_2} = 400K} \right]
WAB=nR  100  .........(1){W_{AB}} = nR\,\,100\,\,.........\left( 1 \right)
Work done for CD is given by
WCD=nR  ΔT{W_{CD}} = nR\,\,\Delta T
  ⟹  WCD=nR(T1−T2)\implies {W_{CD}} = nR\left( {{T_1} - {T_2}} \right)
Putting the values of temperatures
WCD=nR (300−400){W_{CD}} = nR\,\left( {300 - 400} \right)
  ⟹  WCD=nR  100  .......(2)\implies {W_{CD}} = nR\,\,100\,\,.......\left( 2 \right)
Now, the process BC and DA occur at a constant temperature. So BC and DA represent isothermal process and the work done by an isothermal process is given by
W=nRT  ℓn  P1P2W = nRT\,\,\ell n\,\,\dfrac{{{P_1}}}{{{P_2}}}
Where P1{P_1} is the initial pressure
P2{P_2} is the final pressure
Now, work done for isothermal process BC is given by
WBC=nRT  ℓn  P2P1{W_{BC}} = nRT\,\,\ell n\,\,\dfrac{{{P_2}}}{{{P_1}}}
  ⟹  WBC=nRT  ℓn 12  (as  here  P1=2atm,P2=1atm)\implies {W_{BC}} = nRT\,\,\ell n\,\dfrac{1}{2}\,\,\left( {as\,\,here\,\,{P_1} = 2atm,{P_2} = 1atm} \right)
  ⟹  WBC=400nR  ℓn 12  (as  here  T=400K)\implies{W_{BC}} = 400nR\,\,\ell n\,\dfrac{1}{2}\,\,\left( {as\,\,here\,\,T = 400K} \right)
  ⟹  WBC=400nR (ℓn 1−ℓn 2) \implies{W_{BC}} = 400nR\,\left( {\ell n\,1 - \ell n\,2} \right)\,
On solving this we get
WBC=400nR (0−ℓn 2) {W_{BC}} = 400nR\,\left( {0 - \ell n\,2} \right)\,
  ⟹  WBC=400nR  ℓn 2..........(3) \implies {W_{BC}} = 400nR\,\,\ell n\,2..........\left( 3 \right)\,
Now, work done for isothermal process DA is
WDA=nRT  ℓn  21 {W_{DA}} = nRT\,\,\ell n\,\,\dfrac{2}{1}\,
  ⟹  WDA=300nR  ℓn 2  ........(4) \implies{W_{DA}} = 300nR\,\,\ell n\,2\,\,........\left( 4 \right)\,
Total work done =WAB+WBC+WCD+WDA = {W_{AB}} + {W_{BC}} + {W_{CD}} + {W_{DA}}
=100nR−400nRℓn2−100nR+300nRℓn2= 100nR - 400nR\ell n2 - 100nR + 300nR\ell n2
=−100nR  ℓn2= - 100nR\,\,\ell n2
Here number of moles, n=2n = 2
So, Net work done =−100×2  R  ℓn2 = - 100 \times 2\,\,R\,\,\ell n2
=−200R  ℓn2= - 200R\,\,\ell n2

So, the correct answer is “Option A”.

Note:
Remember ℓn(ab)=ℓn  a−ℓn  b\ell n\left( {\dfrac{a}{b}} \right) = \ell n\,\,a - \ell n\,\,b and ℓn  (ab)=ℓn  a +ℓn  b\ell n\,\,\left( {ab} \right) = \ell n\,\,a\, + \ell n\,\,b
So, ℓn(12)=ℓn1−ℓn2\ell n\left( {\dfrac{1}{2}} \right) = \ell n1 - \ell n2that is basic formulas of logarithms are used.