Question
Question: Two moles of Helium gas are to be taken over the cycle \[{\text{ABCDA}}\]as shown (below) in the \[{...
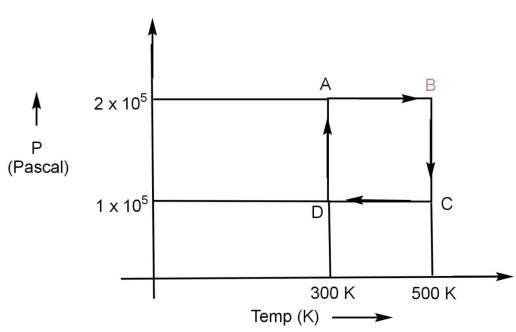
Two moles of Helium gas are to be taken over the cycle ABCDAas shown (below) in the P - Tdiagram. (Assume the gas to be ideal and R is a gas constant.).
Now, match list I with list II and select the option given below:
| List-1| | List-2
---|---|---|---
(P)| Magnitude of the work done by the gas is taking from A to B| (1)| 693 R
(Q)| Magnitude of the work done by the gas is taking from B to C| (2)| 277 R
(R)| Magnitude of the work done by the gas is taking from D to A| (3)| 400 R
(S)| Magnitude of the net heat absorbed/evolved in the cycle ABCDA| (4)| 416 R
A.P - 1, Q - 2, R - 3, S - 4
B.P - 3, Q - 2, R - 4, S - 3
C.P - 3, Q - 1, R - 4, S - 2
D.P - 4, Q - 3, R - 1, S - 2
Solution
Hint: This question is based on the thermodynamic process. The process A to B and C to D is an isobaric process. The process B to C and D to A are isothermal processes. We need to use the required formula of work in each of the cases and we will get work done for each process.
Formula used:
For isobaric process W = - nR(T2−T1)
Where, W is work done, n is number of moles, R is universal gas constant and T2 and T1 are final and initial temperature respectively.
For isothermal process W = - 2.303nRT logP2P1
Where, W is work done, n is number of moles, R is universal gas constant and P2 and P1 are final and initial pressure respectively.
Complete step by step answer:
Let us understand the diagram first:
On the x axis of the graph temperature in K has been plotted and on y axis pressure in Pahas been plotted. So this is a P - T curve. The coordinates of points will give us the value of volume and pressure. If we look at the diagram point A cuts x axis at point 300 that means the temperature of gas at point A will be TA = 300 K and it cut y axis at point 2×105, so the pressure at point A will be PA=2×105 Pa. Similarly we can do this for other, let us write down the value of temperature and pressure at every stage:
TA = 300 K and PA=2×105 Pa
TB = 500 K and PB=2×105 Pa
TC = 500 K and PC=1×105 Pa
TD = 300 K and PD=1×105 Pa
Using the respective equations for the process happening we will calculate the work done as follow:
The process A→B is isobaric:
WA→B=nR(T2−T1)
⇒WA→B=2R(500−300)=400R
The process B→C is isothermal process:
WB→C=−2.303nRT logP2P1
⇒WB→C=−2.303×2×R×500 log1×1052×105=−693R
The process C→D is isobaric:
WC→D=nR(T2−T1)
⇒WC→D=2R(300−500)=−400R
The process D→A is isothermal process:
WD→A=−2.303nRT logP2P1
⇒WD→A=−2.303×2×R×300 log2×1051×105=416R
Total work done can be calculated by adding all the four work which will come out to be
W=400R−693R−400R+416R=−277R
All the above data matches well with option C.
Note:
Isobaric process is the process in which the pressure remains constant; since bar is a unit of pressure we can easily remember that in isobaric process pressure remains constant. Isothermal process is the process in which temperature remains constant. We will ignore the negative sign here because this indicates the direction of reaction and heat changes.
