Question

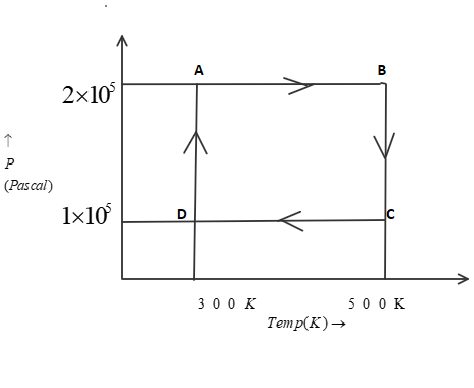
Two moles of helium gas are taken over the cycle $ABCDA$, as shown below in the $P - T$ diagram. (Assume the gas to be ideal and $R$ is gas constant).
Now, match List $I$ with List $II$ and select the options given below:

List $I$	List $II$
(P)	Magnitude of work done on the gas in taking from $A \to B$
(Q)	Magnitude of work done on the gas in taking from $B \to C$
(R)	Magnitude of work done on the gas in taking from $D \to A$
(S)	Magnitude of the net heat absorbed/evolved in the cycle $ABCDA$

A.) $P - 1,Q - 2,R - 3,S - 4$
B.) $P - 3,Q - 2,R - 4,S - 1$
C.) $P - 3,Q - 1,R - 4,S - 2$
D.) $P - 4,Q - 3,R - 1,S - 2$

Answer 1

When temperature remains constant and other parameters change then this process is called an isothermal process and when pressure remains constant then this process is known as an isobaric process.

Complete step by step answer:
There are some thermodynamic processes that are used in this question. These are:
An isobaric process is a thermodynamic process in which pressure remains constant and volume is expanded or contracted. The work done in an isobaric process can be given by the formula as follows:
${W_{isobaric}} = - nR({T_2} - {T_1})$
Where, $n =$ number of moles
$R =$ Real gas constant
${T_2} =$ final temperature
${T_1} =$ Initial temperature
An isothermal process is a thermodynamic process in which the temperature of a system remains constant and pressure may increase or decreases. The work done in an isothermal process can be given as:
${W_{isothermal}} = - 2.303nRT\log \left( {\dfrac{{{P_1}}}{{{P_2}}}} \right)$
Where, ${P_1} =$ Initial pressure
${P_2} =$ Final pressure
$n =$ number of moles
$R =$ Real gas constant
Now, In part P.) to find work done from $A \to B$we know that pressure is constant as we move from point $A$ to point $B$. Therefore, it is an isobaric process. So, we can use this equation:
${W_{isobaric}} = - nR({T_2} - {T_1})$
As given in question, that number of moles($n$) is $2$, also the initial temperature(${T_1}$) is $300K$ and final temperature (${T_2}$) is $500K$. Now, by putting all these values in above equation, we get:
${W_{A \to B}} = - 2R(500 - 300) \\\ = - 400R \\\$

Now, In part Q.) to find work done from $B \to C$ we know that temperature is constant as we move from point $B$ to point $C$. Therefore, it is an isothermal process. So, we can use this equation:
${W_{isothermal}} = - 2.303nRT\log \left( {\dfrac{{{P_1}}}{{{P_2}}}} \right)$
As given in question, that number of moles($n$) is $2$, also the initial pressure(${P_1}$) is $2 \times {10^5}P$ and final pressure (${P_2}$) is $1 \times {10^5}P$. Now, by putting all these values in above equation, we get:
${W_{B \to C}} = - 2.303 \times 2R \times 500 \times \log \left( {\dfrac{{2 \times {{10}^5}}}{{1 \times {{10}^5}}}} \right)$
$= - 693R$
Now, In part R.) to find work done from $D \to A$ we know that temperature is constant as we move from point $D$ to point $A$. Therefore, it is an isothermal process. So, we can use this equation:
${W_{isothermal}} = - 2.303nRT\log \left( {\dfrac{{{P_1}}}{{{P_2}}}} \right)$
As given in question, that number of moles($n$) is $2$, also the initial pressure(${P_1}$) is $1 \times {10^5}P$ and final pressure (${P_2}$) is $2 \times {10^5}P$. Now, by putting all these values in above equation, we get:
${W_{B \to C}} = - 2.303 \times 2R \times 300 \times \log \left( {\dfrac{{1 \times {{10}^5}}}{{2 \times {{10}^5}}}} \right)$
$= + 416R$
Now to find work done from $C \to D$we know that pressure is constant as we move from point $C$ to point $D$. Therefore, it is an isobaric process. So, we can use this equation:
${W_{isobaric}} = - nR({T_2} - {T_1})$
As given in question, that number of moles($n$) is $2$, also the initial temperature(${T_1}$) is $500K$ and final temperature (${T_2}$) is $300K$. Now, by putting all these values in above equation, we get:
${W_{C \to D}} = - 2R(300 - 500) \\\ = + 400R \\\$
Now, to find net heat evolved or absorbed, we will add all work done in the cycle $ABCDA$.
Therefore, Net heat $= {W_{A \to B}} + {W_{B \to C}} + {W_{C \to D}} + {W_{D \to A}}$
$= ( - 400) + ( - 693) + ( + 400) + ( + 416) \\\ = - 277R \\\$
Hence, Option C.) is the correct answer.

Note: Remember that in this question we are asked to find the magnitude of the work done or heat evolved or released. Therefore, we will take all work done and heat evolved or released as positive to get the required answer.