Question

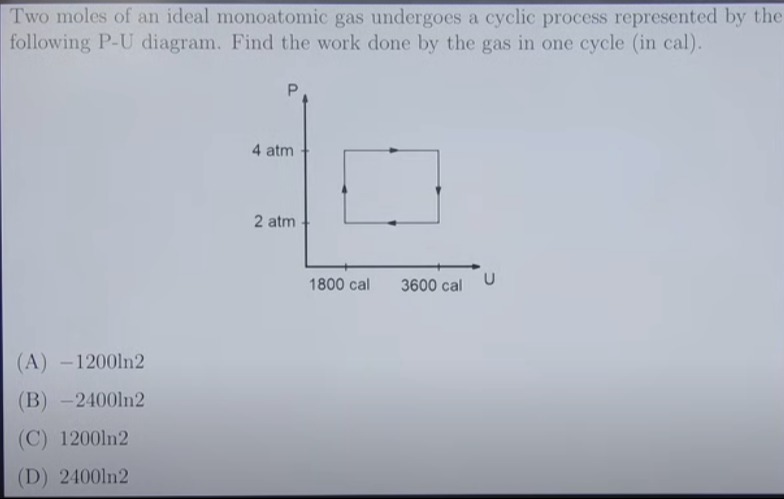
Two moles of an ideal monoatomic gas undergoes a cyclic process represented by the following P-U diagram. Find the work done by the gas in one cycle (in cal).

• A. -1200ln2
• B. -2400ln2
• C. 1200ln2
• D. 2400ln2

Answer 1

Answer: (A)

-1200ln2

Answer 2

The problem asks for the work done by two moles of an ideal monoatomic gas undergoing a cyclic process shown on a P-U diagram.

For an ideal monoatomic gas, the internal energy $U$ is related to pressure $P$ and volume $V$ by the equation: $U = \frac{3}{2} nRT$

Also, from the ideal gas law, $PV = nRT$. Substituting $nRT$ into the internal energy equation, we get: $U = \frac{3}{2} PV$

From this, we can express volume $V$ as: $V = \frac{2U}{3P}$

Let's identify the coordinates of the four corners of the cycle from the P-U diagram: Point A: $(U_1, P_1) = (1800 \text{ cal}, 2 \text{ atm})$ Point B: $(U_2, P_1) = (3600 \text{ cal}, 2 \text{ atm})$ Point C: $(U_2, P_2) = (3600 \text{ cal}, 4 \text{ atm})$ Point D: $(U_1, P_2) = (1800 \text{ cal}, 4 \text{ atm})$

Now, let's calculate the volume at each point using $V = \frac{2U}{3P}$: $V_A = \frac{2 \times 1800 \text{ cal}}{3 \times 2 \text{ atm}} = \frac{3600}{6} \frac{\text{cal}}{\text{atm}} = 600 \frac{\text{cal}}{\text{atm}}$ $V_B = \frac{2 \times 3600 \text{ cal}}{3 \times 2 \text{ atm}} = \frac{7200}{6} \frac{\text{cal}}{\text{atm}} = 1200 \frac{\text{cal}}{\text{atm}}$ $V_C = \frac{2 \times 3600 \text{ cal}}{3 \times 4 \text{ atm}} = \frac{7200}{12} \frac{\text{cal}}{\text{atm}} = 600 \frac{\text{cal}}{\text{atm}}$ $V_D = \frac{2 \times 1800 \text{ cal}}{3 \times 4 \text{ atm}} = \frac{3600}{12} \frac{\text{cal}}{\text{atm}} = 300 \frac{\text{cal}}{\text{atm}}$

The cyclic process consists of four steps as indicated by the arrows: A $\to$ B $\to$ C $\to$ D $\to$ A.

1. Process A to B (Isobaric expansion): Pressure $P$ is constant at $P_1 = 2 \text{ atm}$. Work done $W_{AB} = P_1 (V_B - V_A)$ $W_{AB} = 2 \text{ atm} \times (1200 - 600) \frac{\text{cal}}{\text{atm}} = 2 \times 600 \text{ cal} = 1200 \text{ cal}$

2. Process B to C (Isothermal compression): Internal energy $U$ is constant at $U_2 = 3600 \text{ cal}$. For an ideal gas, constant $U$ implies constant temperature $T$ (isothermal process). Work done $W_{BC} = nRT \ln\left(\frac{V_C}{V_B}\right)$ From $U = \frac{3}{2} nRT$, we have $nRT = \frac{2}{3} U$. So, $nRT = \frac{2}{3} \times 3600 \text{ cal} = 2400 \text{ cal}$. $W_{BC} = 2400 \text{ cal} \times \ln\left(\frac{600}{1200}\right) = 2400 \ln\left(\frac{1}{2}\right) = -2400 \ln(2) \text{ cal}$

3. Process C to D (Isobaric compression): Pressure $P$ is constant at $P_2 = 4 \text{ atm}$. Work done $W_{CD} = P_2 (V_D - V_C)$ $W_{CD} = 4 \text{ atm} \times (300 - 600) \frac{\text{cal}}{\text{atm}} = 4 \times (-300) \text{ cal} = -1200 \text{ cal}$

4. Process D to A (Isothermal expansion): Internal energy $U$ is constant at $U_1 = 1800 \text{ cal}$. This is an isothermal process. Work done $W_{DA} = nRT \ln\left(\frac{V_A}{V_D}\right)$ From $U = \frac{3}{2} nRT$, we have $nRT = \frac{2}{3} U$. So, $nRT = \frac{2}{3} \times 1800 \text{ cal} = 1200 \text{ cal}$. $W_{DA} = 1200 \text{ cal} \times \ln\left(\frac{600}{300}\right) = 1200 \ln(2) \text{ cal}$

Total work done in one cycle: The total work done by the gas in one cycle is the sum of the work done in each process: $W_{cycle} = W_{AB} + W_{BC} + W_{CD} + W_{DA}$ $W_{cycle} = 1200 \text{ cal} + (-2400 \ln(2) \text{ cal}) + (-1200 \text{ cal}) + (1200 \ln(2) \text{ cal})$ $W_{cycle} = (1200 - 1200) + (-2400 \ln(2) + 1200 \ln(2))$ $W_{cycle} = 0 - 1200 \ln(2) \text{ cal}$ $W_{cycle} = -1200 \ln(2) \text{ cal}$

The work done by the gas in one cycle is $-1200 \ln(2)$ cal.