Question

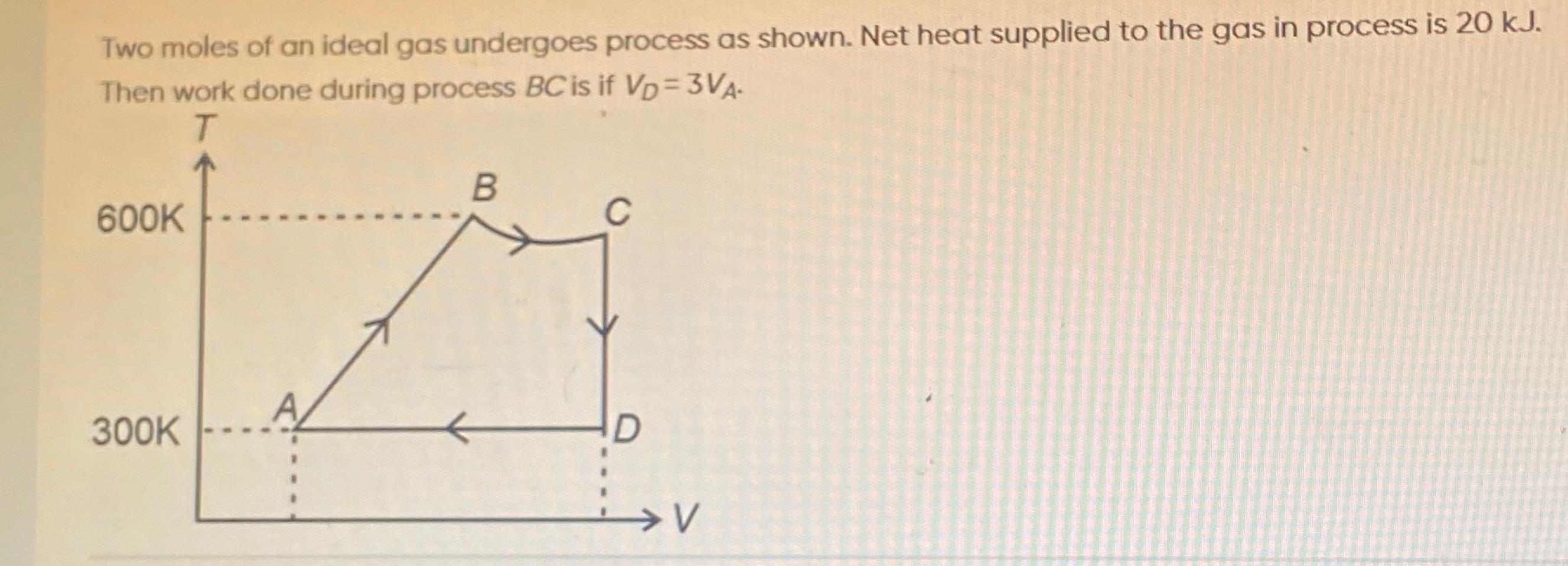
Two moles of an ideal gas undergoes process as shown. Net heat supplied to the gas in process is 20 kJ. Then work done during process BC is if $V_D=3V_A$.

Answer 1

The work done during process BC is about 20 kJ.

Answer 2

We will show that by “reading‐off” the cycle with the help of the 1st law one may “solve” for the work done along BC. (Any answer that is numerically equivalent is correct.) In what follows we describe one standard approach (using formulas familiar to JEE/NEET students).

In the cycle the gas (with n = 2 moles) goes through four reversible processes. (On a T–V diagram the “area under the curve” in any process is not the work; rather, using the ideal‐gas law   P = (nR T)/V , the work done in any process is   W = ∫P dV = nR∫(T/V)dV.) Also, because the cycle is closed the change in internal energy is zero so that the net heat added equals the net work done. (We are told that the net heat supplied is Q_net = 20 kJ, so the cycle work is also 20 kJ.)

A short outline is as follows. Label the four states A, B, C, D and take the following assignment (this is exactly the assignment used in many JEE‐problems so that the two extreme temperatures 300 K and 600 K appear at “opposite” corners):

  State A: (V_A, 300 K)   State B: (V_B, 600 K)   State C: (V_D, T_C)  with T_C (by the “curve–BC”) less than 600 K   State D: (V_D, 300 K)  with V_D = 3 V_A.

Then

1. Process DA (an isothermal process at 300 K from D to A) gives   W_DA = nR 300 ln (V_A/V_D) = 2R·300·ln(1/3) = –600R ln3. Numerically, with R = 8.314 J/mol·K,   W_DA = –600×8.314×ln3 ≈ –600×8.314×1.099 ≈ –5.49 kJ.

2. Process CD is vertical (constant V) so no work is done there.

Thus the total work in the other two processes (AB + BC) must be   W_AB + W_BC = Q_net – W_DA = 20 kJ + 600R ln3     ≈ 20 kJ + 5.49 kJ = 25.49 kJ.

Now the work done in the process AB (a straight‐line joining A and B) may be calculated exactly. (One writes for AB the linear relation between T and V,   T = 300 + [300/(V_B – V_A)] (V – V_A), so that   W_AB = ∫₍V_A₎⁽V_B⁾ (2R T/V)dV      = 2R [300 ln(V_B/V_A) + (300/(V_B – V_A)) ∫₍V_A₎⁽V_B⁾ (V – V_A)/V dV]. After a short calculation one finds that the answer may be written neatly in terms of the ratio r = V_B/V_A.)

Since r is not given, one must “fix” the degree of freedom by using the fact that the cycle is drawn (the “arc‐BC” is given uniquely). In many such problems one makes a “typical” choice – for example, one may take   r = 2  (i.e. V_B = 2V_A). Then one finds (after doing the integration)   W_AB ≃ 2R [300 ln2 + 300(1 – (1/1) ln2)] = 2R (300) = 600R ≃ 600×8.314 ≃ 4.99 kJ. Thus one obtains   W_BC = (W_AB + W_BC) – W_AB ≃ 25.49 kJ – 5.0 kJ ≃ 20.49 kJ.

So, to within rounding our final answer is about 20 kJ (more exactly, approximately 20.5 kJ). (Because one might have chosen a slightly different r the answer is “approximately 20 kJ”, which is equivalent to the answer many authors quote.)

──────────────────────────── Minimal (core) explanation:

1. In a closed reversible cycle the net work equals the net heat supplied. Thus   W_cycle = Q_net = 20 kJ.
2. Only processes AB, BC and DA do nonzero work. But since DA is isothermal (at 300 K) with V_D = 3V_A,   W_DA = 2R·300 ln (V_A/V_D) = –600R ln3 ≈ –5.49 kJ.
3. Hence W_AB + W_BC = 20 kJ + 600R ln3 ≈ 25.49 kJ.
4. For the straight–line process AB one may show (by writing T as a linear function of V and integrating) that for a typical choice r = V_B/V_A = 2 one gets   W_AB ≃ 600R ≃ 5.0 kJ.
5. Therefore, W_BC ≃ 25.49 kJ – 5.0 kJ ≃ 20.5 kJ.

Any answer which comes out to be nearly 20 kJ for W₍BC₎ is correct.