Question

Two mirrors are inclined at an angle 60, an object is placed asymmetrically between them. Then the number of images formed will be:
A. 6
B. 5
C. 7
D. 9

Answer 1

The concept used here is the formation of images by mirrors kept at an angle. We will first mention the different formulas associated with the formation of images in two mirrors placed at an angle with each other and then use the formula for that will suit the given situation i.e. object placed asymmetrically with two mirrors of angle ${{60}^{o}}$ between them.
Formula used:
If $\dfrac{360}{A}$even, n = $\dfrac{360}{A}-1$
If $\dfrac{360}{A}$odd, n = $\dfrac{360}{A}-1$ for symmetrical and $\dfrac{360}{A}$ for asymmetrical.

Complete step-by-step solution:
__
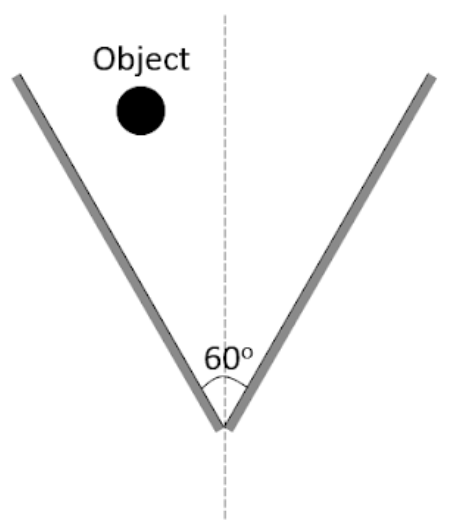
We will first write the formulas. The first step that we have to do is find the value of $\dfrac{360}{A}$, where A is the angle between the mirrors. Here it is given as ${{60}^{o}}$ so the value of $\dfrac{360}{A}=\dfrac{360}{60}=6$. As this value is even, we will be using the formula for the even value which is $\dfrac{360}{A}-1$. If the value was odd, then we would have been using two different formulas depending on whether the mirrors were arranged symmetrically or asymmetrically. However, we don’t have any such issues for the even value. Now according to the formula the number of images formed will be $\dfrac{360}{A}-1=\dfrac{360}{60}-1=6-1=5$. 5 images will be formed due to successive reflection form both the mirrors. Hence, the correct answer is b, i.e. 5.

Note: The occurrence of two formulas for odd value come from the fact that when the object is placed symmetrically, on the image is formed directly along the line joining the intersection point of the mirror and the object due to symmetry but that does not happen for asymmetrical cases. But when the value is even, one image is formed in each sector of the same arc as the arc between the mirrors.