Question

Two metal pieces having a potential difference of 800V are 0.02m apart horizontally. A particle of mass $1.96 \times {10^{ - 15}}kg$ is suspended in equilibrium between the plates. If e is the elementary charge, then charge on the particle is-

A.)8e
B.)6e
C.)e
D.)3e

Answer 1

Hint: We will consider that as the elementary charge is given as e, it will mean that the total charge will be in the multiples e. we will also take the help of a figure. We will apply the formula for electric force.

Complete step by step answer:
Formula used: $E = \dfrac{V}{d}$, $F = Ee = mg$.

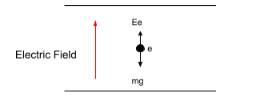
If the charge on the particle is given as e, then there must be an electric force working on the particle which will be Ee.

$\Rightarrow F = Ee$

Since the particle is suspended in an equilibrium, then the electric force mentioned above must be balancing the force mg.

$\Rightarrow F = Ee = mg$

Now, as we know that electric field is equal to $\dfrac{V}{d}$, this gives us-

$\Rightarrow E = \dfrac{V}{d} \\\ \\\ \Rightarrow E = \dfrac{{800}}{{0.02}} \\\ \\\ \Rightarrow E = 40000 \\\ \\\ \Rightarrow E = 4 \times {10^4}V/m \\\$

Now, substituting this value in the equation $F = Ee = mg$, and the value of mass is already given to us by the question.

In the question, e is given as the elementary charge which means that the lowest unit will be in the multiples of e or that the total charge will be in the multiples of e. Thus, we will represent its charge with (ne). we will get-

$\Rightarrow Ee = mg \\\ \\\ \Rightarrow 4 \times {10^4} \times ne = 1.96 \times {10^{ - 15}} \times 9.8 \\\ \\\ \Rightarrow ne = \dfrac{{1.96 \times {{10}^{ - 15}} \times 9.8}}{{4 \times {{10}^4}}} \\\$

Now, the value of n will be the number of electrons. And as we know, the value of e is $1.6 \times {10^{ - 19}}$. Thus, we get-

$\Rightarrow ne = \dfrac{{1.96 \times {{10}^{ - 15}} \times 9.8}}{{4 \times {{10}^4}}} \\\ \\\ \Rightarrow n = \dfrac{{1.96 \times {{10}^{ - 15}} \times 9.8}}{{4 \times {{10}^4} \times 1.6 \times {{10}^{ - 19}}}} \\\ \\\ \Rightarrow n = \dfrac{{196 \times {{10}^{ - 15}} \times 98}}{{4 \times {{10}^4} \times 16 \times {{10}^{ - 17}}}} \\\ \\\ \Rightarrow n = \dfrac{{196 \times {{10}^{ - 15}} \times 98 \times {{10}^{17}} \times {{10}^{ - 4}}}}{{4 \times 16}} \\\ \\\ \Rightarrow n = \dfrac{{196 \times 98 \times {{10}^{ - 2}}}}{{4 \times 16}} \\\ \\\ \Rightarrow n = 300 \times {10^{ - 2}} \\\ \\\ \Rightarrow n = 3 \\\ \\\$

Hence, our answer is 3e.
Thus, we can say that option D is the correct option.

Note: The difference in electrical potentials is the amount of work done to transport a unit charge in an electrical field from one point to another. The difference in the electrical potential of the two charged bodies is known as the potential difference.