Question

Two men on either side of a temple of $30m$ height observe its top at angles of elevation $30{}^\circ$ and $60{}^\circ$ respectively. Find the distance between the two men.

Answer 1

We will first assume that the two men are at points $A$ and $B$ and the top of the temple is at the point $C$. Now will connect these points thus forms a Triangle $ABC$. Now in the problem they have mentioned the angle made by the two men with the top of the temple i.e. the $\angle CAB$ and $\angle CBA$ are given. Now the height of the temple with his top at point $C$ will be represented by the altitude of the triangle $ABC$. To find the distance between the points $A$ and $B$ we will divide the triangle $ABC$ into Two triangles and then we will use trigonometric ratios.

Complete step-by-step answer:
Given that, Two men on either side of a temple of $30m$ height observe its top at angles of elevation $30{}^\circ$ and $60{}^\circ$ respectively.
Let the first man is at the point $A$ and the second man is at the point $B$ and the top of the table is placed at the point $C$. Now from the given data we can plot the points and connected, then the diagram looks like below

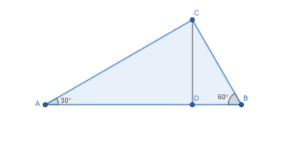
Here $CD$ is the height of the temple and its values is given by $CD=30m$
To find the distance between the points $A$ and $B$, from the above diagram we need to calculate the distance between $AD$ and $DB$.
Consider the triangle $ACD$.
We know
$\tan \theta =\dfrac{\text{Adjacent side to }\theta }{\text{Opposite side to }\theta }$
Then
$\begin{aligned} & \tan \left( \angle CAD \right)=\dfrac{AD}{CD} \\\ & \Rightarrow \tan \left( 30{}^\circ \right)=\dfrac{AD}{30} \\\ & \Rightarrow AD=30\sqrt{3}m....\left( \text{i} \right) \\\ \end{aligned}$
Now considering the triangle $CDB$
$\begin{aligned} & \tan \left( \angle CBD \right)=\dfrac{CD}{DB} \\\ & \Rightarrow \tan \left( 60{}^\circ \right)=\dfrac{30}{DB} \\\ & \Rightarrow DB=\dfrac{30}{\sqrt{3}} \\\ & \Rightarrow DB=10\sqrt{3}m...\left( \text{ii} \right) \\\ \end{aligned}$
Now the value of $AB$ from the diagram is
$AB=AD+DB$
From equations $\left( \text{i} \right)$ and $\left( \text{ii} \right)$, we will get
$\begin{aligned} & AB=30\sqrt{3}+10\sqrt{3} \\\ & AB=40\sqrt{3}m \\\ \end{aligned}$
Now the distance between the two men is $40\sqrt{3}m$.

Note: For this kind of problem the direction of men with respect to the temple is important. If they both lies on same side of the temple and viewing at different angle, then the diagram is given below

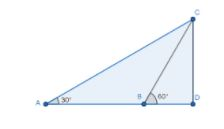
Now the distance between the points $AB$ is given by
$\begin{aligned} & AB=AD-BD \\\ & \Rightarrow AB=CD\tan 30{}^\circ -CD\tan 60{}^\circ \\\ & \Rightarrow AB=30\sqrt{3}-30\times \dfrac{1}{\sqrt{3}} \\\ & \Rightarrow AB=30\sqrt{3}-10\sqrt{3} \\\ & \Rightarrow AB=20\sqrt{3}m \\\ \end{aligned}$