Question

Two men each of mass $m$ stand on the rim of a horizontal circular disc, diametrically opposite to each other. The disc has a mass $M$ and is free to rotate about a vertical axis passing through its centre of mass. Each man starts simultaneously along the rim clockwise and reaches their original starting points on the disc. The angle turned through by the disc with respect to the ground (in radian) is:
A. $\dfrac{{8m\pi }}{{4m + M}}$
B. $\dfrac{{2m\pi }}{{4m + M}}$
C. $\dfrac{{m\pi }}{{M + m}}$
D. $\dfrac{{4m\pi }}{{2M + m}}$

Answer 1

In order to answer this question, to know about the angle turned through by the disc with respect to the ground in radian we will first find out the distance moved by the two men. Then we will use the concept of conservation of angular momentum.

Formula used:
${L_{men}} = {L_{disc}}$
$\Rightarrow {I_1}{\omega _1} = {I_2}{\omega _2}$ $\left[ {\because L = I\omega } \right]$
Here,
$\Rightarrow I = {r^2}m \\\ \Rightarrow \omega = \dfrac{v}{r}$

Complete step by step answer:

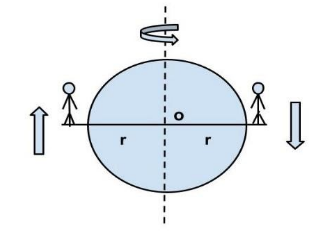
Given that the masses of two men are $m$ each. Mass of disc = $M$
Let us suppose the disc is turned by an angle $\theta$ in an anticlockwise direction.Therefore, angular momentum of the system (men + disc) must be conserved as there is no external force present.

[The rotational equivalent of linear momentum is angular momentum in physics. Because it is a conserved quantity—the total angular momentum of a closed system remains constant—it is a significant quantity in physics.]
Therefore,
${L_{men}} = {L_{disc}}$
$\Rightarrow 2 \times \left( {m{R^2}} \right) \times 2\pi - \theta = \dfrac{{M{R^2}}}{2} \times \theta \\\ \Rightarrow 4\pi m - 2M\theta = \dfrac{M}{2} \times \theta \\\ \therefore \theta = \dfrac{{8m\pi }}{{4m + M}}$
Hence the angle turned by the disc with respect to ground is $\dfrac{{8m\pi }}{{4m + M}}$.

So, the correct option is A.

Note: Angular momentum (like other quantities) is described as an operator in quantum mechanics, with quantized eigenvalues for one-dimensional projections. The Heisenberg uncertainty principle applies to angular momentum, which states that only one projection (also known as a "component") can be measured with absolute precision at any given time; the other two remain unknown. As a result, a quantum particle's rotational axis is indeterminate.