Question

Two men are walking along a horizontal straight line in the same direction. The man in front walks at a speed of $1m{s^{ - 1}}$ and the man behind walks at a speed of $2m{s^{ - 1}}$. A third man is standing at a height $12m$ above the same horizontal line such that all three men are in a vertical plane. The two walking men are blowing identical whistles which emit a sound of frequency $1430Hz$. The speed of sound in air is $330m{s^{ - 1}}$. At the instant when the moving men are $10m$ apart, the stationary man is equidistant from them. The frequency of beats in Hz, heard by the stationary man at this instant is _______.

Answer 1

Here, we need to calculate the apparent frequencies due to moving person A and moving person B, in order to obtain the solution for this problem. An apparent frequency is the frequency that is perceived by an observer. It may or may not be equal to that of actual frequency, the true frequency of the wave.

Formula Used:
The formulae we will be using are:
1. ${F_{Apparent}} = \left( {\dfrac{{c \pm {v_r}}}{{c \pm {v_s}}}} \right){F_o}$
2. $\Delta F = {F_A} - {F_B}$

Complete step by step answer:
Let us draw the picture of the scenario when both moving persons are equidistant from the centre line of the 3rd person standing above.

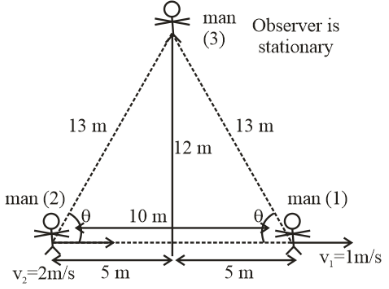
Here the Doppler Effect is taken into account. The Doppler Effect (or the Doppler shift) is the change in frequency of a wave in relation to an observer who is moving relative to the wave source. The reason for the Doppler Effect is that when the source of the waves is moving towards the observer which in the above case is stationary, each successive wave crest is emitted from a position closer to the observer than the crest of the previous wave.
Mathematically if we write the Doppler Effect by naming the following:
Apparent frequency of A = ${F_A}$
Apparent frequency of B = ${F_B}$
Medium of sound in the medium = $c$
Velocity of the receiver relative to the medium = ${v_r}$
Velocity of the source relative to the medium = ${v_s}$
Emitted frequency = ${F_o}$
${F_{Apparent}} = \left( {\dfrac{{c \pm {v_r}}}{{c \pm {v_s}}}} \right){F_o}$
So in this case we have,
${F_A} = \left( {\dfrac{{330}}{{330 - 2\cos \theta }}} \right)1430$……………………….(i)
Also from the given diagram we have $\cos \theta =\dfrac{5}{{13}}$
Again for B we can write the Doppler Effect equation as,
${F_B} = \left( {\dfrac{{330}}{{330 + 1\cos \theta }}} \right)1430$…………………………...(ii)
Now from binomial expansion theory we can expand equation i and ii and it gives,
${F_A} = \left( {1 + \dfrac{{2\cos \theta }}{{330}}} \right)1430$
$\Rightarrow {F_B} = \left( {1 - \dfrac{{\cos \theta }}{{330}}} \right)143$
Now the change in frequency will be the frequency of beats in Hz. heard by the stationary man at this instant.
$\Delta F = {F_A} - {F_B} \\\ \Rightarrow \Delta F = 1430\left( {\dfrac{{3\cos \theta }}{{330}}} \right)$
Now we already have the value of ${\cos \theta}$ and further simplifying we get the frequency as-
$\Delta F = \dfrac{{1430\cos \theta }}{{110}} \\\ \Rightarrow \Delta F = 13\cos \theta \\\ \Rightarrow \Delta F = 13 \times \dfrac{5}{{13}} \\\ \therefore \Delta F = 5$

The required frequency is $5Hz$.

Note: While doing calculations involving Binomial expansion, the higher order terms in the binomial expansion were neglected as these value will have insignificant effect on the calculation.Remember that, the velocity of the receiver relative to the medium ($[{v_r}]$) will have positive value if receiver is moving towards the source whereas negative if receiver moving in opposite direction of the source. Similarly, the velocity of the source relative to the medium ($[{v_s}]$), is positive if source is moving away from the receiver whereas it will be negative if source is moving towards the receiver.