Question

Two men A and B running with velocities $5\hat{i}m{{s}^{-1}}$ and $-5\hat{i}m{{s}^{-1}}$ respectively. The rain is falling vertically downwards with a velocity of $-5\sqrt{3}\hat{j}m{{s}^{-1}}$. In order to be safe from rain in which direction they should keep their umbrellas?
A. both should keep the umbrella $60{}^\circ$ from the positive x-axis.
B. both should keep the umbrella $120{}^\circ$ from the positive x-axis.
C. man A should place the umbrella at $60{}^\circ$ and B at $120{}^\circ$ from the positive x-axis.
D. man A should place the umbrella at $120{}^\circ$ and B at $60{}^\circ$ from the positive x-axis.

Answer 1

Umbrella should be kept in a direction where the rainfall comes towards the men. Draw the diagram showing the directions of the velocities. Then after the analysis of the diagram, find the angle between the vectors using the tangent of the angle. This all will help you in answering this question.

Complete step by step answer:
Umbrella should be kept in a direction where the rainfall comes towards the men. The resultant of the velocities of the men should be found. The rainfall is having a velocity with respect to men can be written as,
${{\vec{V}}_{rm}}={{\vec{V}}_{r}}-{{\vec{V}}_{m}}$
Where ${{\vec{V}}_{r}}$ be the velocity of the rainfall and ${{\vec{V}}_{m}}$ be the velocity of the man.

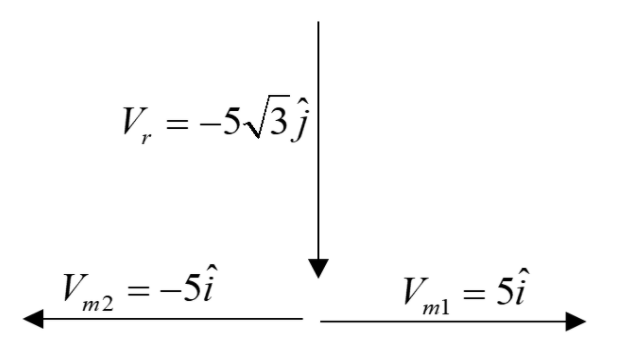
Now let us consider the first case.

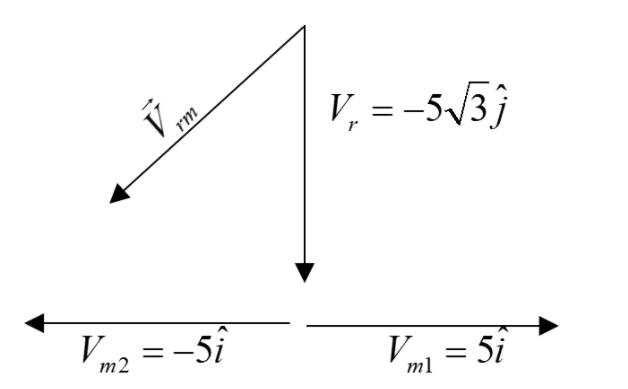
The umbrella should be placed in the direction of the relative velocity between the rainfall and the men.
Now let us look at the second case.

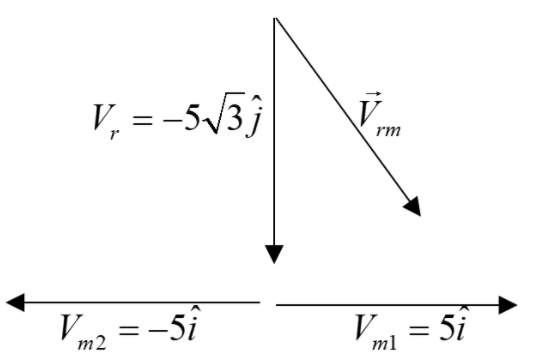
Here also the umbrella should be placed in the direction of the relative velocity between the rainfall and the men.
The angle between the vectors can be found by taking the tangent of the vectors. That is,
$\tan \theta =\dfrac{\left| {{{\vec{V}}}_{m}} \right|}{\left| {{{\vec{V}}}_{r}} \right|}$
The magnitude of velocity of the rain has been given as,
$\left| {{{\vec{V}}}_{r}} \right|=5\sqrt{3}m{{s}^{-1}}$
And that of the men can be written as,
$\left| {{{\vec{V}}}_{m}} \right|=5m{{s}^{-1}}$
Substituting the values in it will give,
$\begin{aligned} & \tan \theta =\dfrac{\left| {{{\vec{V}}}_{m}} \right|}{\left| {{{\vec{V}}}_{r}} \right|}=\dfrac{5}{5\sqrt{3}}=\dfrac{1}{\sqrt{3}} \\\ & \Rightarrow \tan \theta =\dfrac{1}{\sqrt{3}} \\\ & \Rightarrow \theta =30{}^\circ \\\ \end{aligned}$
Now let us substitute this value in the case of Man A and man B.
Man A can be shown as,

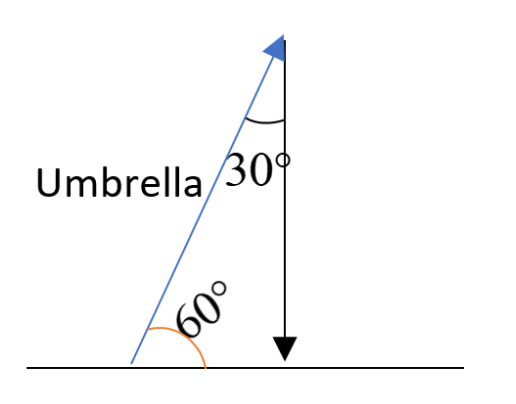
Man B can be shown as,

The needed angle is shown in red colour.

So, the correct answer is “Option C”.

Note: Velocity is the time rate of variation of displacement. The relative velocity is the velocity felt by an observer who is in another frame of reference with respect to the moving frame. Relative velocity sometimes can be zero even if the actual value of the velocities are not zero.