Question

Two men $A$ and $B$ are standing on the opposite edge of a long platform, which is further kept on a smooth floor. They start moving towards each other and finally meet at the midpoint of the platform. Find displaced of the platform if the mass of $A$, platform and $B$ are $40Kg$, $50Kg$ and $60Kg$ respectively.

Answer 1

In this case, we need to consider the center of mass. As no external force is applied, the center of mass remains constant. Using the concept of center of mass, we can find the displacement of the platform.

Complete step by step answer:
Let us draw the diagram from the data given in the question; it looks like this:

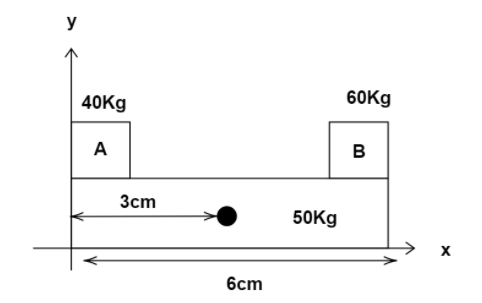
The distance of the object $A$ from the X-axis is zero, the distance of the center of mass of the platform is $3cm$ , and the distance of the center of mass of the object $B$ from the x-axis is $6cm$.
Therefore, the center of mass can be obtained as:
${d_{cm}} = \dfrac{{40 \times 0 + 50 \times 3 + 60 \times 6}}{{40 + 50 + 60}}$
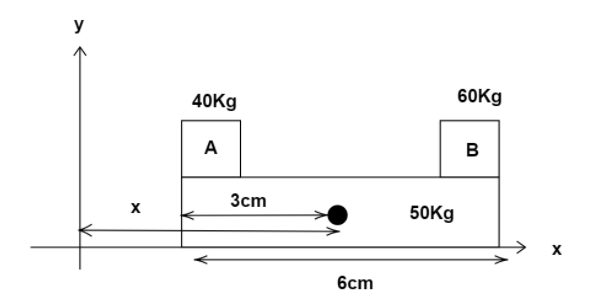
Now, after displacement, let the displacement of the platform from the x-axis is $x$
Since the displacement occurs in the X-axis, the distance of the center of mass for each object changes.
The change is depicted in the diagram below:
$\dfrac{{40 \times 0 + 50 \times 3 + 60 \times 6}}{{40 + 50 + 60}} = \dfrac{{60 \times x + 50 \times (3 + x) + 40 \times (6 + x)}}{{40 + 60 + 50}}$
On solving the equation, we obtain

The new center of mass of the system can be written as:
${d_{cm}} = \dfrac{{60 \times x + 50 \times (3 + x) + 40 \times (6 + x)}}{{40 + 60 + 50}}$
Equating the two centers of mass, we get:
As no external force is acting on the objects, the center of mass of the system must remain the same.
$\dfrac{{40 \times 0 + 50 \times 3 + 60 \times 6}}{{40 + 50 + 60}} = \dfrac{{60 \times x + 50 \times (3 + x) + 40 \times (6 + x)}}{{40 + 60 + 50}}$
On solving this, we get
${d_{cm}} = 0.8m$

Note: The physical significance of the center of mass can be understood as the point on which the entire mass of the body lies. It is also the point on which the object can be balanced. For some objects the center of mass of the body lies inside the body, whereas in the case of others, the center of the body lies outside the object. This is observed in the case of a ring.