Question
Question: Two masses \({\text{A}}\) and \({\text{B}}\) of \({\text{10kg}}\) and \({\text{5kg}}\) respectively ...
Two masses A and B of 10kg and 5kg respectively are connected within a string passes over a frictionally pulley fixed at a corner of a table. As shown in figure. The Coefficient of A with the table is 0.20. The minimum value of mass of C that may be placed on the on A to prevent it from moving is equal to:
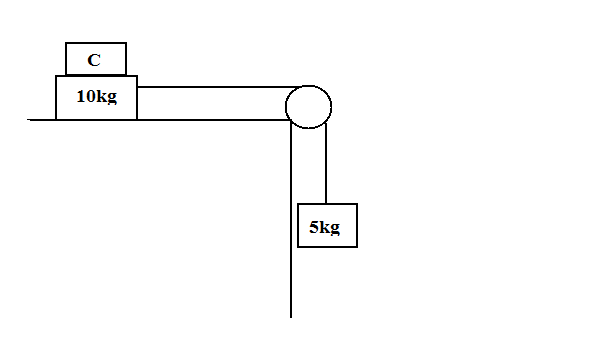
A) 15kg
B) 10kg
C) 5kg
D) 0kg
Solution
The block will not move unless a force greater than the maximum friction is applied to it. The maximum friction will be the product of the coefficient of static friction times the normal force acting on the block due to the contact surface.
Formula Used::
f1=μN
∵f1 is maximum friction
μ is coefficient of static friction
N is the Normal Reaction.
Complete step by step Answer:
Let the mass of block C is Mc,
And tension on a rope is T
Now let us draw the free body diagram for the given situation, this will help us balance all the forces acting on the body.
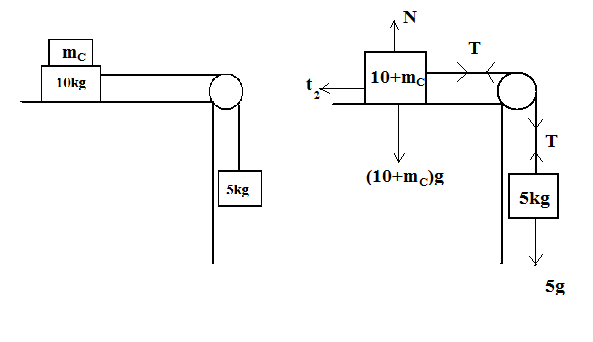
According to the question, we have to find the minimum value of block C. So that block A prevents itself from moving.
By seeing Free Body Diagram, We get that the tension T is balancing the mass 5kg.
So, we can write
T−5g=0 Or
T=mg T=5g
T=5g−(i)
Secondly, the friction f1 is balancing the Tension T, So.
f1−T=0 f1=T−(ii)
The Normal Reaction is balancing the masses of blocks {\text{C & A}}. So
N=(10+Mc)g−(iii)
Now, we know that, friction can be given as;
f1=μN
Putting the value of N from eqn(iii)
f1=μ(10+mc)g
Further from equation (ii) we get;
T=μ(10+mc)g
[∵f1=T]
Now from equation (i)
5g=μ(10+mc)g
Now calculating further we get;
⇒5=μ(10+mc)
⇒μ5=(10+mc)
⇒0.25=(10+mc)
∴mc=15kg
So, the minimum value of block C such that it prevents block Afrom moving is 15kg.
Hence, Option (A) is correct, i.e. 15kg.
Note: The simple way to solve these types of questions is to make a free body diagram of the system, make equations of resulting force and find out the value of quantity which is asked in a question. i.e. Net force =0 [Newton’s 3rd law].
