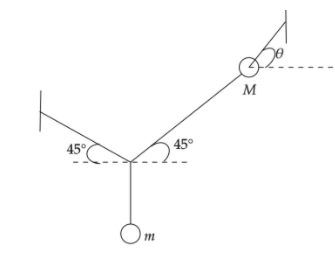
Question

Two masses m and M are attached with string, for the system to be in equilibrium we have

Answer 1

First we will draw a rough diagram and represent each body in its free body diagram. Then resolve each tensile force. Then equate summation of each coordinate to zero for each of the masses. On further solving we can find the angle at which mass M is attached.

Complete step by step answer:
As per the problem we have two masses m and M are attached with string, for the system to be in equilibrium.
We have to now calculate the angle $\theta$ as shown in the figure.

Free body diagram of mass m,

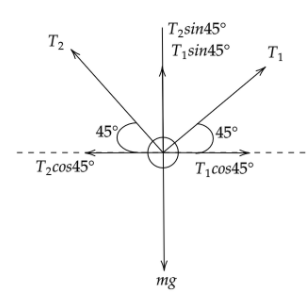
Now from the figure on resoling along the y coordinate we will get,
$\sum {{F_y} = 0}$
Now we can write,
${T_2}\sin 45^\circ + {T_1}\sin 45^\circ - mg = 0$
On further solving we will get,
$\dfrac{{{T_2}}}{{\sqrt 2 }} + \dfrac{{{T_1}}}{{\sqrt 2 }} = mg$
$\Rightarrow {T_2} + {T_1} = \sqrt 2 mg \ldots \ldots \left( 1 \right)$
Now from the figure on resoling along the y coordinate we will get,
$\sum {{F_x} = 0}$
Now we can write,
${T_1}\cos 45^\circ - {T_2}\cos 45^\circ = 0$
On further solving we will get,
$\dfrac{{{T_2}}}{{\sqrt 2 }} = \dfrac{{{T_1}}}{{\sqrt 2 }}$
$\Rightarrow {T_2} = {T_1} \ldots \ldots \left( 2 \right)$
Now putting equation (1) in place of equation (2) we will get,
${T_1} + {T_1} = \sqrt 2 mg$
$\Rightarrow 2{T_1} = \sqrt 2 mg = \dfrac{{mg}}{{\sqrt 2 }}$
Free body diagram of mass M,

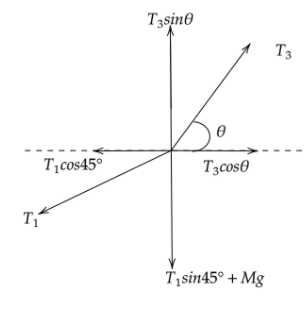
Now from the figure on resoling along the y coordinate we will get,
$\sum {{F_y} = 0}$
Now we can write,
${T_3}\sin \theta - \left( {{T_1}\sin 45^\circ + Mg} \right) = 0$
On further solving we will get,
${T_3}\sin \theta = \left( {\dfrac{{{T_1}}}{{\sqrt 2 }} + Mg} \right) \ldots \ldots \left( 3 \right)$
Now from the figure on resoling along the y coordinate we will get,
$\sum {{F_x} = 0}$
Now we can write,
${T_3}\cos \theta - {T_1}\cos 45^\circ = 0$
On further solving we will get,
${T_3}\cos \theta = {T_1}\cos 45^\circ$
$\Rightarrow {T_3}\cos \theta = \dfrac{{{T_1}}}{{\sqrt 2 }} \ldots \ldots \left( 4 \right)$
Taking the ratio of equation (3) to (4) we will get,
$\dfrac{{{T_3}\sin \theta }}{{{T_3}\cos \theta }} = \dfrac{{\left( {\dfrac{{{T_1}}}{{\sqrt 2 }} + Mg} \right)}}{{\dfrac{{{T_1}}}{{\sqrt 2 }}}}$
Cancelling the common term we will get,
$\tan \theta = \dfrac{{\left( {\dfrac{{{T_1}}}{{\sqrt 2 }} + Mg} \right)}}{{\dfrac{{{T_1}}}{{\sqrt 2 }}}}$
Putting the value of ${T_1}$ in the above equation we will get,
$\tan \theta = \dfrac{{\left( {\dfrac{{mg}}{2} + Mg} \right)}}{{\dfrac{{mg}}{2}}}$
Cancelling the common term we will get,
$\tan \theta = 1 + \dfrac{{2M}}{m}$

Note: Here we have used the free body diagram to solve the problem. Remember that the free body diagram is usually associated with the motion of a free body which is a pictorial device used by the physicist and the engineers so as to solve the problem easily and to analyze the problem.