Question
Question: Two masses m and \(\dfrac{m}{2}\) are connected at the two ends of a massless rigid rod of length l....
Two masses m and 2m are connected at the two ends of a massless rigid rod of length l. The rod is suspended by a thin wire of torsional constant k at the centre of mass of the rod-mass system (see figure). Because of torsional constant k, the restoring torque is τ=kθ for angular displacement θ. If the rod is rotated by θ0 and released, the tension in it when it passes through its mean position will be:
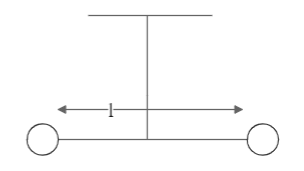
(A) l3kθ02
(B) 2lkθ02
(C) l2kθ02
(D) lkθ02
Solution
Hint
For a two mass system such as this one, the total force would act on the centre of mass of the system. So when a torsion is applied, the tension generated can be found on the centre of the mass.
Formula used: T=rmv2, where T is the tension generated and is equal to the centrifugal force generated by mass m moving with velocity v, and at a distance of r from the axis.
Complete step by step answer
In this question, we have two unequal masses connected by a rod. The road is then rotated by some angle which causes a restoring torque to appear. This torque will be responsible for generating a tension in the road, and this is what we are required to find out. The information provided to us includes:
Two masses m and 2m
Torsional constant: k
Restoring torque τ=kθ
Angular displacement of the rod: θ0
Let us assume the centre of mass of the system is at x distance from the LHS mass. Since the distance between the two masses is l, the distance x from mass 2m, will be given as:
x=2m+m2m×0+m×l=3m2ml=32l
Hence, from the RHS mass m, the distance of the centre of mass will be:
r=l−32l=3l
We know that the tension generated in the rod will be equal to the outward centrifugal force, hence:
T=rmv2
Here, the velocity of rotation is unknown to us. We know the angular displacement, hence along the arc made by r, the velocity will be:
v=(rθ0)ω=3lθ0ω where ω is the frequency of the torsional pendulum created.
We know that this frequency can be given us:
ω=Ik
Where k is the torsional constant and I is the moment of inertia. We calculate this moment of inertia as:
I=Ml2 where M is the reduced mass of the system and l is the distance between the two.
This reduced mass for our case will be given as:
M=2m+m2m×m=23m2m2=3m
This gives us the moment of inertia of the rotating system as:
I=3ml2
Now, putting these values to calculate the tension, we get:
T=rmv2=3lm(3lθ0ω)2
On solving further:
T=m3lθ02ω2
Substituting the value of ω gives us:
T=m3Ilθ02k=m3ml2lθ02k3=lθ02k
Hence, the correct answer is option (D).
Note
In this question, the centrifugal force acts on the rod because of its moment of inertia. This inertia along with the force is generated due to the circular motion of the rod, and is directed away from the centre around which the body is rotating which is the centre of the mass.
