Question

Two masses ${m_1}$ and ${m_2}$ ( ${m_1} > {m_2}$ ) are connected by a massless flexible and inextensible string passed over a massless and frictionless pulley. The acceleration of centre of mass is:
A) ${\left( {\dfrac{{{m_1} - {m_2}}}{{{m_1} + {m_2}}}} \right)^2}g$
B) $\dfrac{{{m_1} - {m_2}}}{{{m_1} + {m_2}}}g$
C) $\dfrac{{{m_1} + {m_2}}}{{{m_1} - {m_2}}}g$
D) Zero

Answer 1

The mass of the first block is more than the mass of the second block. The first block will move downward and the second block will move in upward direction with the same acceleration but in the opposite direction. Calculate the acceleration of each block.

Using the formula of centre of mass, the acceleration of the centre of mass can be calculated.

Complete step by step solution:
We are given that the mass of the first block is greater than the second block thus, the first block having mass ${m_1}$ will move downward with some acceleration.

As, both the blocks are connected with a string thus, the second block will move in an upward direction with the same magnitude of acceleration.
Let us draw the FBD of the given system.

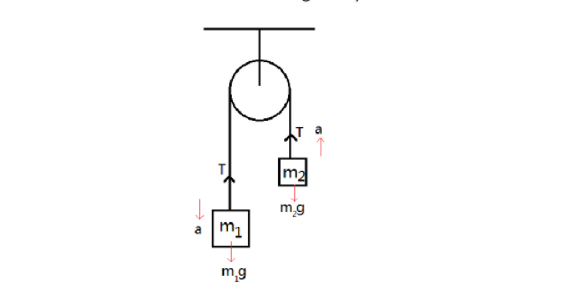
Diagram: Self-made
From the diagram, $T$ is the tension force and $a$ is the acceleration of the masses.
The forces on first mass are
${m_1}g - T = {m_1}a$
$\Rightarrow T = {m_1}g - {m_1}a$
The forces on second mass are
$T - {m_2}g = {m_2}a$

$\Rightarrow T = {m_2}g + {m_2}a$

As the tension force acting on both the masses is equal therefore, we have:
${m_1}g - {m_1}a = {m_2}g + {m_2}a$
$\Rightarrow {m_1}g - {m_2}g = {m_2}a + {m_1}a$
$\Rightarrow ({m_1} - {m_2})g = ({m_1} + {m_2})a$
$\Rightarrow a = \dfrac{{({m_1} - {m_2})g}}{{({m_1} + {m_2})}}$

This is the magnitude of the acceleration of the masses.
The acceleration of the centre of mass ${a_{cm}}$ is given as
${a_{cm}} = \dfrac{{({m_1}{a_1} + {m_2}{a_2})}}{{({m_1} + {m_2})}}$
Here ${a_1},{a_2}$ are the acceleration of ${m_1},{m_2}$ respectively.
But we have ${a_1} = a$ taking downward acceleration as positive and ${a_2} = - a$ thus
substituting the values of acceleration, we get
${a_{cm}} = \dfrac{{\left[ {{m_1}\left( {\dfrac{{({m_1} - {m_2})g}}{{({m_1} + {m_2})}}} \right) + {m_2}\left( { - 1} \right)\left( {\dfrac{{({m_1} - {m_2})g}}{{({m_1} + {m_2})}}} \right)} \right]}}{{({m_1} \+ {m_2})}}$
$\Rightarrow {a_{cm}} = \dfrac{{\left[ {\left( {{m_1} - {m_2}} \right)\left( {\dfrac{{({m_1} - {m_2})g}}{{({m_1} + {m_2})}}} \right) + \left( {\dfrac{{({m_1} - {m_2})g}}{{({m_1} + {m_2})}}} \right)} \right]}}{{({m_1} + {m_2})}}$
$\Rightarrow {a_{cm}} = {\left[ {\dfrac{{\left( {{m_1} - {m_2}} \right)}}{{\left( {{m_1} + {m_2}} \right)}}} \right]^2}g$
This is the acceleration of the centre of mass of the given system.

Therefore, option A is the correct option.

Note: The mass will move in the opposite direction and thus, they will have acceleration in the opposite direction with the same magnitude. The tension force acting on both the masses will be equal. The pulley is given to be massless. If the masses were equal, their acceleration would be zero.