Solveeit Logo
Login

Question

Question: Two masses \({{m}_{1}}\) and \({{m}_{2}}\) are connected by a massless string. Find the value of ten...

Two masses m1{{m}_{1}} and m2{{m}_{2}} are connected by a massless string. Find the value of tension in the string if a force of 200 N is applied

Explanation

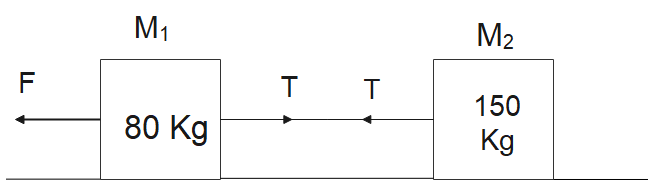
Solution

Tension is defined in physics as the pulling force transmitted axially by a string, cable, chain, or other one-dimensional continuous component, or by each end of a rod, truss member, or other three-dimensional object; tension may also be defined as the action-reaction pair of forces acting at each end of said elements. Tension can be thought of as the polar opposite of compression.

Complete step by step solution:
In this question we need to find the value of Tension (T), and we have been given that
Mass of Block m1{{m}_{1}}= 80 Kg
Mass of Block m2{{m}_{2}} = 150 Kg
Force Applied (F) = 200 N
Now, we know that force is given by the formula
F = m.a
But in this question, we have two masses, therefore, force will be written as
F = (m1{{m}_{1}}+ m2{{m}_{2}}) a
Where “a” is the acceleration
Now, putting the values of both the masses and the force applied we can find the acceleration
200 N = (80+150) a
On solving this, we get
a=1.15 ms−2a=1.15\text{ m}{{\text{s}}^{-2}}
Now, as we can see in the figure that the string is attached in between mass m1{{m}_{1}} and m2{{m}_{2}}. Also the applied force is in the left direction, therefore the tension will be only due to the mass m2{{m}_{2}}
So, we can write
Tension (T) = m2{{m}_{2}}(a)
Putting the values, we get
Tension (T) = (150) (1.15)
Therefore, Tension (T) = 173 N
Hence, this is the required solution for this question.

Note: The force exerted by the ends of a three-dimensional, continuous object, such as a rod or truss member, is also known as tension. Under strain, such a rod elongates. The force per cross-sectional area, rather than the force alone, determines the amount of elongation and the load that will cause failure.