Question

Two masses $m_1 = 5kg$ and $m_2 = 10kg$ ,connected by an inextensible string over frictionless pulley, are moving as shown in the figure. The coefficient of friction of the horizontal surface is $0.15$. The minimum weight $m$ that should be put on the top of $m_2$ to stop the motion is:

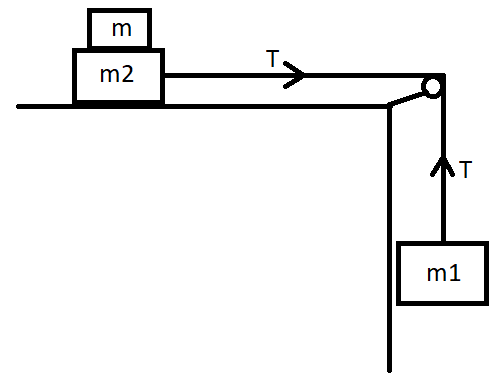
A) $43.3kg$
B) $10.3kg$
C) $18.3kg$
D) $27.3kg$

Answer 1

Just remember if we want to stop the movement of any part in a mechanical arrangement, the net force acting on them must be in an equilibrium manner. So consider the system as in equilibrium condition to solve this problem.

Complete step by step answer:
First of all define all the data given in the question,
$m_1 = 5kg$
$m_2 = 10kg$
Coefficient of friction, $\mu = 0.15$
For solving this problem, we consider this whole mechanical arrangement is in equilibrium condition; and we are considering the equilibrium condition separately for the hanging mass ( that is, $m_1$) and the mass placed on the table (that is, $m_2 + m$)
Net force acting on the hanging mass:
We know, a string followed by a frictionless pulley is holding the mass $m_1$ in an equilibrium state, that is, no movement is happening to mass $m_1$ . As it is hanged, the forces acting on that mass will be in an upward direction or downward direction. Here the force acting on the mass $m_1$ are gravitational force which is in downward direction and the tension on the string which is the upward direction. As the mass $m_1$ is in equilibrium, these forces are equal, that is,
$T = m_1 \times g$ …………………………. (Eqn. 1)
Here, $T =$Tension Acting on the string, $g =$Gravitational constant
Net force acting on the mass placed on the table:
Here we consider the mass $m_2\& m$ as a single mass $(m_2 + m)$ . The forces acting on $(m_2 + m)$ are Frictional force and the tension on the spring. As the mass $(m_2 + m)$ is in equilibrium, these forces are equal and opposite.
Frictional force acting on mass$(m_1 + m)$, $f$ equals,
$f = \mu \times N$
Here, $N$- Normal force acting on mass $(m_2 + m)$ which is equal to,
$N = (m_2 + m) \times g$
$\therefore f = \mu \times (m_2 + m) \times g$
We already know, the frictional force is equals to the tension on the string,
$\therefore T = f = \mu \times (m_2 + m) \times g$
Applying the value of $T$from (Eqn.1), we get,
$T = \mu \times (m_2 + m) \times g = m_1 \times g$
$g$ gets cancelled and applying the other values we get,
$\Rightarrow 0.15 \times (10 + m) = 5$
$\Rightarrow 10 + m = \dfrac{5}{{0.15}}$
$\Rightarrow m = \dfrac{5}{{0.15}} - 10$
$\Rightarrow m = 23.33kg$
Now we get the minimum mass which should be placed above mass $m_2$ is $23.33kg$.
The mass placing above $m_2$ should be equal or greater than $23.33kg$.
So, the final answer is Option(D).

Note: When we are dealing with the problems of these types, take the net forces acting on the mechanical arrangement as zero. The coefficient of friction is a dimensionless quantity. Do not apply all the values in the early steps, as some of the values may get cancelled later. This will help to reduce the difficulty.