Question

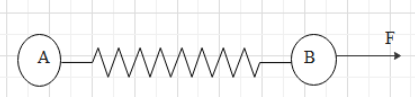
Two masses A and B of mass M are fixed together with a massless spring. A force acts on a mass B as shown in figure. At the instant shown, the mass A has acceleration a. What is the acceleration of mass B?

& \text{A}\text{. }\dfrac{F}{M}-a \\\ & \text{B}\text{. }a \\\ & \text{C}\text{. }-a \\\ & \text{D}\text{. }\dfrac{F}{M} \\\ \end{aligned}$$

Answer 1

Here we have given a system where two bodies of mass M are attached to each other by massless spring. When force is applied on mass B then there is an acceleration experienced by A as it is attached to B. Similarly, there will be acceleration associated by B which we have to calculate. By balancing the forces and tension we can find the acceleration of B.

Complete answer:

As we can see from the diagram that the only force here is due to the force applied on B. But due to F there will be some tension T in the spring and this tension is for both A and B as both are attached to spring.

Let us consider the body of mass A, it is given that when force is applied on mass B then mass A has acceleration, a and the only force which is experienced by mass A is due to tension in spring. Hence we can write
$T=Ma\text{ }...............\text{(i)}$
Here M is the mass of A.
Now for the mass B there will be force F applied on it and the tension in the spring, if the acceleration of B is a’, then by balancing the forces we get
$F-T=Ma'$
Substituting value of T from equation (i) we get

& F-Ma=Ma' \\\ & \Rightarrow a'=\dfrac{F-Ma}{M} \\\ & \Rightarrow a'=\dfrac{F}{M}-a \\\ \end{aligned}$$ Hence acceleration of B in terms of force, mass and acceleration of A is$$\dfrac{F}{M}-a$$. **Option A is the correct answer.** **Note:** Here we didn’t consider the downward pull of gravity as the whole system is experiencing force and tension in the horizontal direction. We can also say that the whole system experienced the same gravitational pull as the mass of bodies are mass and spring is massless due to which it nullifies the effect of gravitational force.