Question

Two masses A and B of 15kg and 10kg are connected with a string passing over a frictionless pulley fixed at the corner of a table (as shown in figure). The coefficient of friction between the table and block is 0.4. The minimum mass of the C that may be placed on A to prevent it from moving is

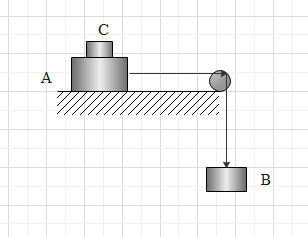
(A). 10kg
(B). 5kg
(C). Zero
(D). 15kg

Answer 1

In this question, tension in the vertical part of string is equal to the gravitational force acting on block B i.e. weight of B. Tension in the horizontal part of string is due to the coefficient of friction between table and combination of mass of both blocks A and C.
Obtain the tension on the string due to mass B. Then obtain the tension on the string due to mass A and B. equate these two equations to find the mass C.

Complete step by step answer:
Let ${{M}_{A}},{{M}_{B}},{{M}_{C}}$ be the masses of blocks A, B and C respectively.
T be the tension in the string. µ be the coefficient of friction between table and the block.
Here, it is given that, ${{M}_{A}}=15kg$, ${{M}_{B}}=10kg$ and $\mu =0.4$
Gravitational force is acting on block B and it equal to
$T={{M}_{B}}g$
Where, g is acceleration due to gravity and its value is $9.8m{{s}^{-2}}$. So, value of T is,
$\begin{aligned} & T=10\times 9.8 \\\ & T=98N \\\ \end{aligned}$
Now, the tension in the string on the table is due to the combination mass of block A and C and the coefficient of friction between table and block. So, we can write,
$T=\mu \left( {{M}_{A}}+{{M}_{C}} \right)\times g$
Putting the values on this equation,
$T=0.4\times \left( 15+{{M}_{C}} \right)\times g$
Equating the above two equations, we get that,
$\begin{aligned} & 98=0.4\times \left( 15+{{M}_{C}} \right)\times 9.8 \\\ & 15+{{M}_{C}}=\dfrac{98}{0.4\times 9.8} \\\ & 15+{{M}_{C}}=25 \\\ & {{M}_{C}}=10kg \\\ \end{aligned}$
So, the mass of the mass C is 10 kg.

So, the correct answer is “Option A”.

Note:
First, try to understand the given system and find out all the forces acting on all masses. It helps to figure out what we have to do and how we can approach the appropriate answer.
Tension can be defined as the pulling force on a string or any flexible length.