Solveeit Logo
Login

Question

Question: Two masses A and B of 10 kg and 5 kg respectively are connected with a string passing over a frictio...

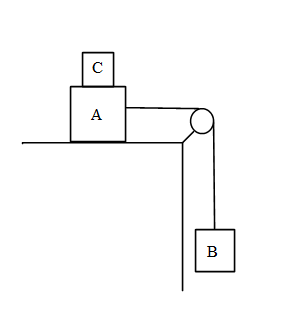
Two masses A and B of 10 kg and 5 kg respectively are connected with a string passing over a frictionless pulley fixed at the corner of a table as in figure. The coefficient of friction of A with the table is 0.2. The minimum mass of C that may be placed on A to prevent it from moving is equal to:

A) 20 kg.
B) 15 kg.
C) 10 kg.
D) 5 kg.
E) 0 kg.

Explanation

Solution

The friction is the resistive force which stops the movement of the body. The friction depends upon the coefficient of friction which is constant for a material and also it depends upon the roughness of the surface.

Formula used:
The formula of the weight is equal to,
⇒W=mg\Rightarrow W = mg
Where mass is m and acceleration due to gravity is g.
The formula of the friction is given by,
⇒f=μ×R\Rightarrow f = \mu \times R
Where the coefficient of friction is μ\mu and the normal reaction is R.

Complete step by step solution:
In this problem it is given that two masses A and B of 10 kg and 5 kg respectively are connected with a string passing over a frictionless pulley fixed at the corner of a table as in figure the coefficient of friction of A with the table is 0.2 and we need to find the minimum mass of C that may be placed on A to prevent it from moving.
The free body diagram of the system.

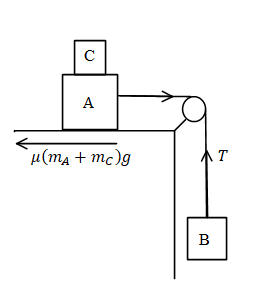
The tension in the string is equal to,
⇒T=mBg\Rightarrow T = {m_B}g
⇒T=5×10\Rightarrow T = 5 \times 10
⇒T=50N\Rightarrow T = 50N
The force that the combination of block A and C is 50 N.
⇒T=μ(mA+mB)g\Rightarrow T = \mu \left( {{m_A} + {m_B}} \right)g
⇒T=0⋅2×(10+mB)×10\Rightarrow T = 0 \cdot 2 \times \left( {10 + {m_B}} \right) \times 10
⇒T=2×(10+mB)\Rightarrow T = 2 \times \left( {10 + {m_B}} \right)
⇒T=20+2mB\Rightarrow T = 20 + 2{m_B}
⇒50=20+2mB\Rightarrow 50 = 20 + 2{m_B}
⇒2mB=30\Rightarrow 2{m_B} = 30
⇒mB=15kg\Rightarrow {m_B} = 15kg
The minimum mass of the block B is equal to 15kg.

The correct answer for this problem is option B.

Note: The students are advised to understand and remember the formula of the friction and also the formula of the weight. The friction force should be equal to the tension of the string so that the combination of block A and C doesn’t move.