Question
Question: Two masses A and B connected with an inextensible string of length l lie on a smooth horizontal plan...
Two masses A and B connected with an inextensible string of length l lie on a smooth horizontal plane. A is given a velocity of v m/s along the ground perpendicular to line AB as shown in the figure. Find the tension in a string during their subsequent motions.
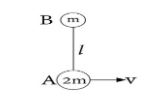
Solution
Here using the concept of center of mass and anybody of mass is attached at one end of the string is whirled in a horizontal circle of the radius then tension in the string is equal to centripetal force.
Formula used:
T=lmv2
Centre of mass coordinate, Y=m1+m2m1y1+m2y2
Complete step-by-step answer:
We need to find out the center of mass of the system. Let's start with the formula as shown below,
Y=m1+m2m1y1+m2y2
Where,
m1=mass of the first body
m2=mass of the second body
y1=Distance of the first body from the center
y2= Distance of second body from the center
Let's substitute the values of m1, m2, y1, y2 in the formula of the center of mass coordinate. We get,
Y=3m2m×0+m×l=3l (From point A.)
For a body, we know that,
Angular momentum is given as, L=mvr
Where, L=angular momentum, m=mass of the body, r= distance between mass and center of mass
Let's substitute the values for the ‘r’ in the angular momentum equation, we get,
L=2m×v×3l=32mvl
From the diagram, we know that the entire length between A and B is divided into l/3 and 2l/3, where l is the length of the string. Thus the entire length between A and B is given as,
l=3l+32l
Let’s move ahead, If ω is the angular velocity gained,
Then, L=LA+LB
Where, LA=angular momentum of mass A, LB= angular momentum of mass B
On substituting values for LA and LB we get,
L=2m(3l)2×ω+m(32l)2ω
Since we know that, L=mvr
We know that, ω=lv .Thus substituting the value of ω in equivalent angular momentum.
Therefore, on solving further the tension in the string,
T=mω2r=(2m)(lv)2×3l
T=3l2mv2
Thus the tension in the string is equal to T=3l2mv2
Additional information:
When a particle moves in a circular path with uniform speed, the direction of its velocity changes at every point on the circumference of the circle continuously. But the magnitude of the velocity remains constant.
Centripetal force is the net or unbalanced force directed toward the center of the circle at any point to deviate the body from its tangential path into a circular path. The direction of the centripetal force is in the direction of centripetal acceleration that is directed along the radius towards the center.
The centripetal force causes centripetal acceleration. The centripetal acceleration changes the direction of the velocity of a particle in a circular motion. If the centripetal force disappears or stops to act a point, then the body flies off tangentially at that point due to the inertia of direction.
During translational motion, of a rigid body, all the constituent particles of the body move along parallel straight lines and undergo equal displacement in the same time interval. Hence, the velocity, as well as the acceleration of every particle in the rigid body during translational motion, is the same.
In the rotational motion of a rigid body, a line of a particle in the body remains fixed and all the other particles describe concentric circles around this fixed line of particles. The fixed-line of particles is called the axis of rotation.
The center of mass of a system particles moves as if the entire mass of the system is concentrated at the center of mass.
Note: In this type of question, find out the center of mass between given two bodies. The important point is that to take a circular path by a string a centripetal force as well as tension in the string is required in the same amount.
A rigid body is a body in which the distance between all pairs of particles does not change during the motion of the body. Hence there is no change in the shape and size of the body during motion under the application of forces.
Due to the application of external forces, a rigid body can have either translational or rotational motion.
