Question

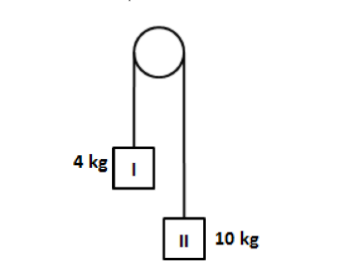
Two masses 4 kg and 10 kg are connected at the ends of a light inextensible string
that goes over a smooth pulley. To block the accelerated motion of the masses the extra
force required is

A. 42 N upward on II
B. 16.8 N down on I
C. Not possible
D. Both (A) and (B)

Answer 1

Draw the free body diagram and use Newton’s second law to express the net force on the masses separately. Equate the two equations to get the acceleration of the masses. If we apply the force of the same magnitude which produces this acceleration in the given mass, we can halt the upward or downward motion of the given mass.

Formula used:
Newton’s second law of motion, ${F_{net}} = ma$, where, m is the mass and a is the
acceleration.

Complete step by step answer:

We have given the two masses ${m_1} = 4\,{\text{kg}}$ and ${m_2} = 10\,{\text{kg}}$.
Let’s draw the free body diagram of the forces acting on the two masses as shown in the
figure below.

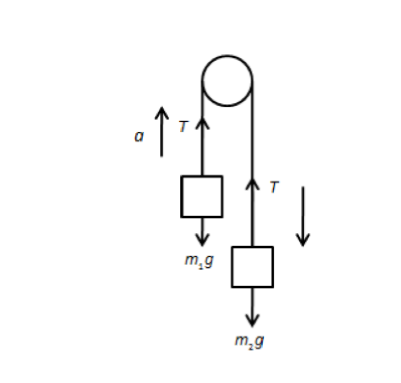
Let’s determine the acceleration of the above system using Newton’s second law as follows,
$T - {m_1}g = {m_1}a$ …… (1)
$T - {m_2}g = - {m_2}a$ …… (2)

Subtracting equation (2) from equation (1), we get,
$- {m_1}g + {m_2}g = {m_1}a + {m_2}a$
$\Rightarrow a = \left( {\dfrac{{{m_2} - {m_1}}}{{{m_1} + {m_2}}}} \right)g$

Substituting ${m_1} = 4\,{\text{kg}}$ and ${m_2} = 10\,{\text{kg}}$, we get,
$a = \left( {\dfrac{{10 - 4}}{{4 + 10}}} \right)g$
$\Rightarrow a = \dfrac{6}{{14}}g$

Now, we have the acceleration of the masses which is the same for both the masses. This
acceleration is upwards for the mass 4 kg and downwards for mass 10 kg. If we apply the
force of the same magnitude which produces the acceleration $a = \dfrac{6}{{14}}g$ in
mass ${m_1}$, we can halt the upward motion of the mass ${m_1}$ and in turn we can
halt the motion of the system.

Therefore,
${F_1} = {m_1}a$
$\Rightarrow {F_1} = \left( 4 \right)\left( {\dfrac{6}{{14}}g} \right)$
$\Rightarrow {F_1} = 16.8\,{\text{N}}$

Thus, the downward force of magnitude 16.8 N can block the accelerated motion of the
masses.

If we apply the force of the same magnitude which produces the acceleration $a = \dfrac{6}{{14}}g$ in mass ${m_2}$, we can halt the downward motion of the mass
${m_2}$ and in turn we can halt the motion of the system.

Therefore,
${F_2} = {m_2}a$
$\Rightarrow {F_2} = \left( {10} \right)\left( {\dfrac{6}{{14}}g} \right)$
$\Rightarrow {F_2} = 42\,{\text{N}}$

Thus, the upward force of magnitude 42 N on the mass II can block the accelerated motion
of the masses.

So, the correct answer is option (D).

Note: The tension in the string is the same on the both sides since the masses are connected to the same string. While defining the direction of the forces acting on the masses, be precise to show the direction of the tension force. The tension force always directed towards the support. In equation (2), we have taken the negative sign for the acceleration since for the mass 10 kg, the acceleration is downwards.