Question

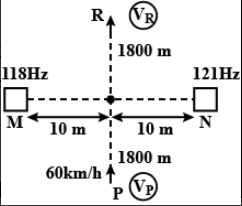
Two loudspeakers $M$ and $N$ are located $20m$ apart and emit sound at frequencies $118\;Hz$ and $121\;Hz$ respectively. A car is initially at a point $P,\;1800\;m$ away from the midpoint $Q$ of the line $MN$ and moves towards Q constantly at $60km{h^{ - 1}}$ along perpendicular bisector of $MN$ . It crosses $Q$ and eventually reaches a point $R,1800$ away from $Q$ . Let $\nu \left( t \right)\;$ represent the beat frequency measured by a person sitting in the car at time $t$ . Let ${v_P}$ ​, ${v_Q}$ and ${v_R}$ be the beat frequencies measured at locations $P,Q,R\;$ respectively. The speed of sound in air is $300m{s^{ - 1}}$ . Which of the following statement (s) is (are) true regarding the sound heard by the person?
(A) A plot below represents schematically the variation of beat frequency with time

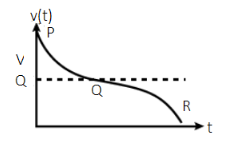
(B) The rate of change in beat frequency is maximum when the car reaches point $Q$ .
(C) ${v_P} + {v_R} = 2{v_Q}$
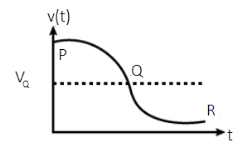
(D) The plot below shows the variation for beat frequency with time.

Answer 1

Hint : In order to solve this question, we are first going to consider all the information given, then after finding the apparent frequencies of the loudspeakers at the distance $P$ and $Q$ , we get the idea of the relation of the frequencies at different points and also the point where the frequency is maximum.

Complete Step By Step Answer:
Here, we are given with the two loudspeakers, $M$ and $N$
Distance between them is, $d = 20m$
Frequency by loudspeaker $M$ , ${\nu _M} = 118Hz$
Frequency for loudspeaker $N$ , ${\nu _N} = 121Hz$
Now the point $P,\;1800\;m$ away from the midpoint $Q$ of the line $MN$ ,

Thus, apparent frequency of $M$ and $N$ at $P$ is:
${\nu _M}' = \dfrac{{v + {v_0}}}{v}{\nu _M}$ ,putting the values of the velocities in this equation, we get
{\nu _M}' = \dfrac{{330 + \dfrac{{50}}{3}}}{{330}} \times 118 \\\ \Rightarrow {\nu _M}' = \dfrac{{1040}}{{990}}118 \\\
Also, ${\nu _N}' = \dfrac{{v + {v_0}}}{v}{\nu _N}$
Putting the values in this equation,
{\nu _N}' = \dfrac{{330 + \dfrac{{50}}{3}}}{{330}} \times 121 \\\ \Rightarrow {\nu _N}' = \dfrac{{1040}}{{990}}121 \\\
Thus, frequency at $P$ is
${\nu _P} = {\nu _M}' - {\nu _N}' = \dfrac{{1040}}{{330}}Hz$
Thus, apparent frequency of $M$ and $N$ at $R$ is:
${\nu _M}' = \dfrac{{v - {v_0}}}{v}{\nu _M}$
Putting the values, we get
{\nu _M}' = \dfrac{{330 - \dfrac{{50}}{3}}}{{330}} \times 118 \\\ \Rightarrow {\nu _M}' = \dfrac{{940}}{{990}}118 \\\
Also, ${\nu _N}' = \dfrac{{v - {v_0}}}{v}{\nu _N}$ ,
Putting values, we get
{\nu _N}' = \dfrac{{330 - \dfrac{{50}}{3}}}{{330}} \times 121 \\\ \Rightarrow {\nu _N}' = \dfrac{{940}}{{990}}121 \\\
Thus, apparent frequency is
${\nu _R} = {\nu _N}' - {\nu _M}' = \dfrac{{940}}{{330}}Hz$
Now, beat frequency at $Q$ is calculated as
${v_Q} = 121 - 118 = 3Hz$
Now, if we check option (C),
{v_P} + {v_R} = 2{\nu _Q} \\\ 6 = 2 \times 3 \\\
Also, $\dfrac{{d\nu }}{{dt}}$ is maximum at $Q$ ,
Hence, the correct options are (B),(C),(D), i.e.,
The rate of change in beat frequency is maximum when the car reaches point $Q$ .
${v_P} + {v_R} = 2{v_Q}$
The plot below shows the variation for beat frequency with time.

Note :
It is important to note that at the point of maximum rate of change of frequency, the double derivative is zero thus, indicating that the point is a maxima point. Also the apparent frequencies at the points at larger distances is less as compared to those points which are nearer.