Question

Two loudspeakers $L_1$ and $L_2$ driven by a common oscillator and amplifier, are arranged. The frequency of the oscillator is gradually increased from zero and the detector at D records a series of maxima and minima. If the speed of sound is $330m/s$ then the frequency at which the first maximum is observed is:

Answer 1

We are asked to find the position of the first central maxima. The concept of interference of waves comes into play in this situation. We can start by drawing a suitable diagram depicting the interference. Then we can use the formulas related to interference and get the position of the first minima. Initially we find the path difference then we can move on to finding the phase change and thus finding the answer to the question.

Formula used: The formula used to find the path difference is given by $\Delta x = \sqrt {{x_1}^2 + {x_2}^2} - {x_2}$
The formula to find the phase change is given by $\delta = \dfrac{{2\pi }}{\lambda }\Delta x$
For first minima $\delta = 2\pi$
The formula to find the frequency is given by $\upsilon = \dfrac{v}{\lambda }$
Where ${x_1}$ and ${x_2}$ are the distances
$\lambda$ is the wavelength
$v$ is the velocity of sound

Complete step by step solution:
Let us start by drawing a rough diagram showing the interference from the information given in the question.

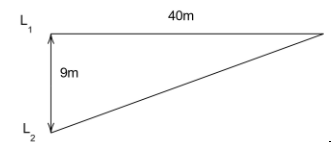
We can write down the values ${x_1} = 9m$
${x_2} = 40m$
$v = 330m/s$
We can now move onto finding the path difference using the formula $\Delta x = \sqrt {{x_1}^2 + {x_2}^2} - {x_2}$
Substituting the values, we get $\Delta x = \sqrt {{x_1}^2 + {x_2}^2} - {x_2} = \sqrt {{9^2} + {{40}^2}} - 40 = 41 - 40 = 1m$
Now we can move onto finding the phase change by using the formula $\delta = \dfrac{{2\pi }}{\lambda }\Delta x$
Substituting the values, we get $\delta = \dfrac{{2\pi }}{\lambda }\Delta x = \dfrac{{2\pi }}{\lambda } \times 1 = \dfrac{{2\pi }}{\lambda }$
We know that for first minima, the value of phase change is $\delta = 2\pi$
Now we can find the value of wavelength by comparison and get $\lambda = 1m$
We can now use the formula $\upsilon = \dfrac{v}{\lambda }$ and find the value of frequency as
$\upsilon = \dfrac{v}{\lambda } = \dfrac{{330m/s}}{{1m}} = 330Hz$

Note:
Interference can be defined as the superposition of two or more waves that form a resultant wave with any amplitude be it greater than, less than or equal to the amplitude of the constituent waves. When the amplitude of the resultant wave is greater than the constituent waves that are of the same wavelength, we have constructive interference. When the amplitude of the resultant waves is lesser than the constituent waves having the same wavelengths, we have destructive interference.