Question

Two longest wavelengths (in nanometre) in the Lyman series of the hydrogen spectrum, are

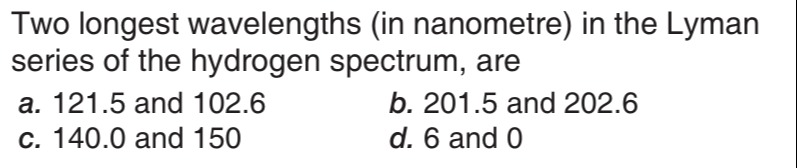
• A. 121.5 and 102.6
• B. 201.5 and 202.6
• C. 140.0 and 150
• D. 6 and 0

Answer 1

Answer: (A)

121.5 and 102.6

Answer 2

The wavelengths in the hydrogen spectrum are given by the Rydberg formula:

$\frac{1}{\lambda} = R \left( \frac{1}{n_{lower}^2} - \frac{1}{n_{higher}^2} \right)$

where $R$ is the Rydberg constant, $n_{lower}$ is the principal quantum number of the lower energy level, and $n_{higher}$ is the principal quantum number of the higher energy level ($n_{higher} > n_{lower}$).

For the Lyman series, the electron transitions to the ground state, so $n_{lower} = 1$. The formula becomes:

$\frac{1}{\lambda} = R \left( \frac{1}{1^2} - \frac{1}{n_{higher}^2} \right) = R \left( 1 - \frac{1}{n_{higher}^2} \right)$

where $n_{higher} = 2, 3, 4, \dots$.

The wavelength $\lambda$ is longest when the energy difference is smallest. The smallest energy difference in the Lyman series corresponds to the transition from the lowest possible higher energy level, which is $n_{higher} = 2$.

The longest wavelength ($\lambda_1$) corresponds to the transition from $n_{higher} = 2$ to $n_{lower} = 1$:

$\frac{1}{\lambda_1} = R \left( 1 - \frac{1}{2^2} \right) = R \left( 1 - \frac{1}{4} \right) = R \left( \frac{3}{4} \right)$

$\lambda_1 = \frac{4}{3R}$

The second longest wavelength ($\lambda_2$) corresponds to the transition from the next lowest higher energy level, which is $n_{higher} = 3$ to $n_{lower} = 1$:

$\frac{1}{\lambda_2} = R \left( 1 - \frac{1}{3^2} \right) = R \left( 1 - \frac{1}{9} \right) = R \left( \frac{8}{9} \right)$

$\lambda_2 = \frac{9}{8R}$

To calculate the wavelengths in nanometers, we use the value of the Rydberg constant $R \approx 1.09677 \times 10^7 \, m^{-1}$.

$\lambda_1 = \frac{4}{3 \times 1.09677 \times 10^7 \, m^{-1}} \approx \frac{4}{3.29031 \times 10^7} \, m \approx 1.21567 \times 10^{-7} \, m$

Converting to nanometers: $1.21567 \times 10^{-7} \, m \times \frac{10^9 \, nm}{1 \, m} \approx 121.567 \, nm$.

$\lambda_2 = \frac{9}{8 \times 1.09677 \times 10^7 \, m^{-1}} \approx \frac{9}{8.77416 \times 10^7} \, m \approx 1.02570 \times 10^{-7} \, m$

Converting to nanometers: $1.02570 \times 10^{-7} \, m \times \frac{10^9 \, nm}{1 \, m} \approx 102.570 \, nm$.

Using a slightly more precise value of R from the similar question, $R = 109678 \, cm^{-1} = 1.09678 \times 10^7 \, m^{-1}$:

$\lambda_1 = \frac{4}{3 \times 1.09678 \times 10^7 \, m^{-1}} \approx 1.21565 \times 10^{-7} \, m = 121.565 \, nm$.

$\lambda_2 = \frac{9}{8 \times 1.09678 \times 10^7 \, m^{-1}} \approx 1.02569 \times 10^{-7} \, m = 102.569 \, nm$.

Rounding these values to one decimal place gives 121.6 nm and 102.6 nm. Comparing with the options, option (a) has values 121.5 and 102.6. These are the closest values.

The two longest wavelengths in the Lyman series are approximately 121.6 nm (from n=2 to n=1) and 102.6 nm (from n=3 to n=1).