Question
Question: Two long straight parallel wires, carrying (adjustable) current \({I_1}\) and \({I_2}\), are kept at...
Two long straight parallel wires, carrying (adjustable) current I1 and I2, are kept at a distance d apart. If the force ′F′ between the two wires is taken as ‘positive’ when the wires repel each other and ‘negative’ when the wires attract each other, the graph showing the dependence of ′F′, on the product I1I2, would be
(A)
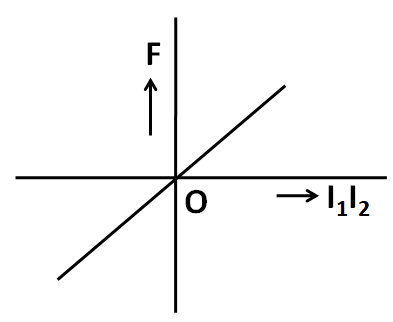
(B)
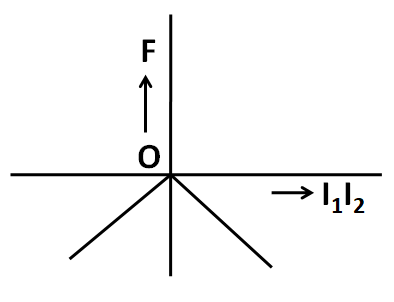
(C)
(D)
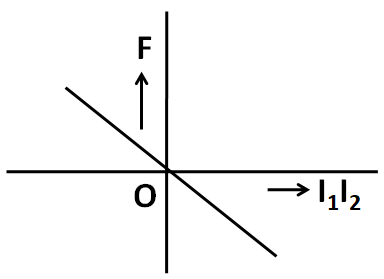
Solution
To solve this question, we need to determine the nature of the force for the parallel and the anti parallel currents. Then using the plot given in the question, we can get the correct plot out of the given options.
Formula used: The formula used to solve this question is given by
F=2πdμ0I1I2, here F is the force between two wires carrying currents I1 and I2, and d is the separation between the wires.
Complete step-by-step solution:
We know that the force between two current carrying wires is given by the formula
F=2πdμ0I1I2
Now, the nature of this force (attractive or repulsive) is decided by the relative signs of the currents I1 and I2. We know that if the two currents are parallel, then the force is attractive in nature, but if the currents are anti parallel, then the force is repulsive in nature.
The parallel currents mean that the product I1I2 is positive. Also, the anti parallel currents mean the product I1I2 is negative.
In the graph given in the options B and C, the sign of the force is not changing with the sign of the product I1I2.
So both the options B and C are incorrect.
Now, according to the question, the attractive force is taken as negative, while the repulsive force is taken as positive. As stated above, when the product I1I2 is positive, then the force is attractive. But when the product I1I2 is negative, then the force is repulsive. So the sign of the force is opposite to the sign of the product I1I2.
Hence, the correct answer is option D.
Note: We need to carefully read the sign convention for the force given in the question. By looking at the formula for the force between two current carrying wires, we may conclude that the sign of the force is the same as that of the product I1I2. But the sign convention given in the question is just opposite to this.
