Question

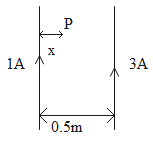
Two long straight parallel conducting wires, kept 0.5m apart, carry 1A and 3A currents, respectively. (i) What is the force acting per unit length of the two wires? (ii) At what position in the plane of the wires, the resultant magnetic field will be zero?

Answer 1

For the first part the force per unit length is calculated using the equation that the ratio of product of permeability of free space and product of both currents to the twice the product of pi and distance between the conducting plates. For the second part, consider that the net magnetic field is zero. Hence substitute the equation for B in the equation for the net magnetic field. Then substitute the values and by rearranging calculate the value of x.

Formula used:
The magnitude of the magnetic field B at a distance d from a straight wire carrying a current I is given by,
$B=\dfrac{{{\mu }_{0}}I}{2\pi d}$
where, B is the magnetic field
${{\mu }_{0}}$ is the permeability of free space
I is the current flowed through it
d is the separating distance.

Complete step by step solution:
(i) $\dfrac{F}{l}=\dfrac{{{\mu }_{0}}{{I}_{1}}{{I}_{2}}}{2\pi d}$
Substituting the values in the equation we get,
$\Rightarrow \dfrac{F}{l}=\dfrac{4\pi \times {{10}^{-7}}\times 1\times 3}{2\pi \times 0.5}$
$\therefore \dfrac{F}{l}=12\times {{10}^{-7}}N/m$
(ii) Let at the point P the magnetic field is zero.
That is, ${{B}_{net}}={{B}_{1}}-{{B}_{2}}=0$
$\Rightarrow {{B}_{1}}={{B}_{2}}$
$\dfrac{{{\mu }_{0}}{{I}_{1}}}{2\pi x}=\dfrac{{{\mu }_{0}}{{I}_{2}}}{2\pi \left( 0.5-x \right)}$
$\Rightarrow \dfrac{{{I}_{1}}}{x}=\dfrac{{{I}_{2}}}{0.5-x}$
Substituting the value of ${{I}_{1}}\And {{I}_{2}}$ we get,
$\dfrac{1}{x}=\dfrac{3}{0.5-x}$
$\Rightarrow 3x=0.5-x$
$\Rightarrow 4x=0.5$
$\begin{aligned} & \Rightarrow x=\dfrac{0.5}{4}=0.125m \\\ & \therefore x=12.5cm \\\ \end{aligned}$
Thus at x=12.5cm position in the plane of the wires, the resultant magnetic field will be zero.

Note: A magnetic field can be described as an influence of magnetic effect on the moving electric charges. Thus a magnetic field is a vector field. The moving charges or currents produce a magnetic field in the surrounding space. Electrostatic field lines always form closed loops. That is, it starts at a positive charge and terminates at a negative charge. Magnetic field lines always form closed loops. Thus the field lines are circles concentric with the wire.