Question

Two long parallel wires carry currents $i$ and $2i$ in the same direction. Magnetic field between the wires is $B$ . If the current in the second wire, $2i$ is switched off, then magnetic field at the same point is:
A) $2B$
B) $B$
C) $\dfrac{B}{2}$
D) $\sqrt {2B}$

Answer 1

Hint
Using the formula to calculate Magnetic field due to infinite wire (long wire) through which current $i$ flows . Try to find the Magnetic field between the given two wires and take the vector sum of the total Magnetic field at that point to say it $B$. Now again calculate the Magnetic field at this point and now try to relate it with $B$ and we will get the answer.

Complete step by step solution
From hint we’ve got the approach what we have to do in the question:
Now, magnetic field due a long wire at a distance $r$ is:
$B = \dfrac{{{\mu _0}I}}{{2\pi r}}$
The direction of the magnetic field can be found by Right Hand Thumb rule.
According to given question, The magnet field due to two wires having currents $i$ and $2i$ is given by:
$B = \dfrac{{{\mu _0}2I}}{{2\pi r}} - \dfrac{{{\mu _0}I}}{{2\pi r}}$
We are subtracting because magnet field due to two wires will be in opposite direction:
$B = \dfrac{{{\mu _0}I}}{{2\pi r}}$

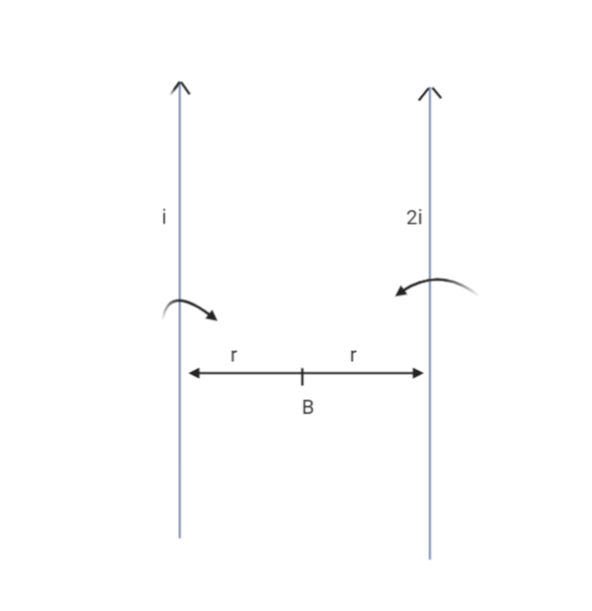
Now, if wire having current having $2i$ is removed then magnetic field at the same point due to $i$ will be:
$B' = \dfrac{{{\mu _0}I}}{{2\pi r}}$
This $B$ and $B'$ are the same.
Thus the answer is option (B).

Note
Whenever you calculate a magnetic field be conscious of the direction of the magnetic field . Magnetic field is calculated as a vector. This is also called Biot-Savart Law. Biot-Savart law is used to calculate the magnetic field due to a thin and straight wire at a particular distance. For better understanding, ketch the magnetic field created from a thin, straight wire by using the second right-hand rule.