Question
Question: Two long parallel wires are at distance 2d apart. They carry steady equal current flowing out of the...
Two long parallel wires are at distance 2d apart. They carry steady equal current flowing out of the plane of the paper as shown. The variation of the magnetic field along the line XX’ is given by:
A. 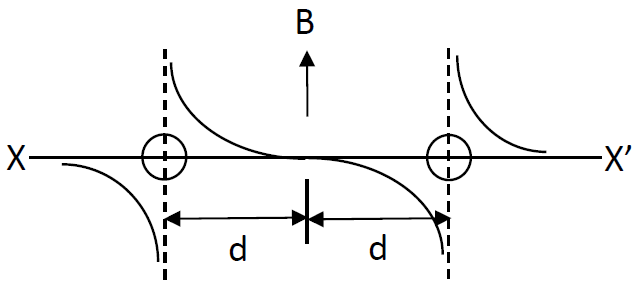
B. 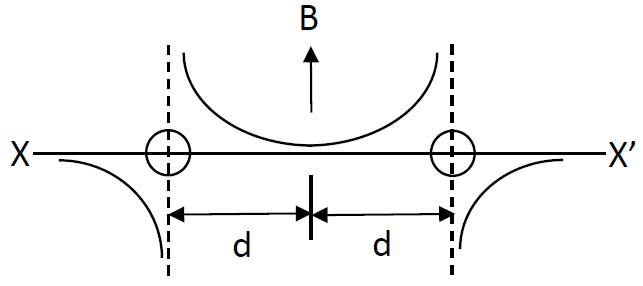
C. 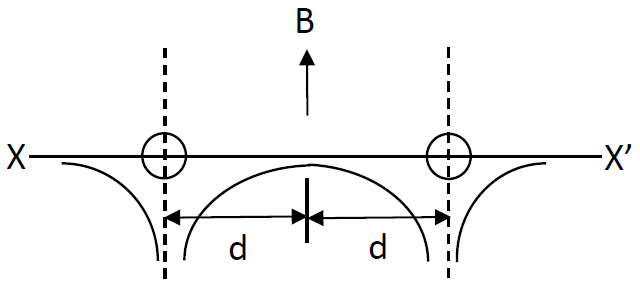
D. 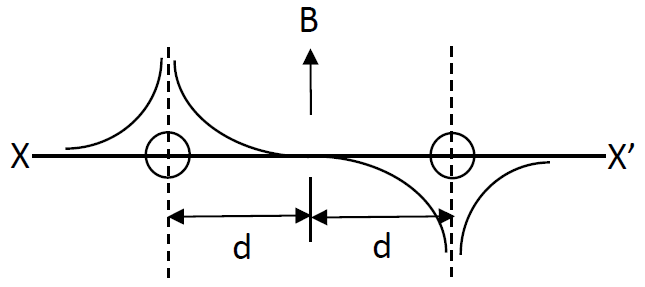
Solution
Hint: Magnetic field lines follow right hand thumb rule and the field value at a location is inversely proportional to the distance from the wire carrying a steady current.
Complete answer:
Consider a single wire carrying current I. The magnetic field at a distance r from the wire is given by:
B=2πrμ0I, where μ0 is a constant. Therefore magnetic field at a location is inversely proportional to the distance from the current carrying wire. Here they have given us two wires carrying current in the direction out of the plane of paper. By right hand thumb rule with thumb denoting the direction of the current through the wire, the magnetic field lines will be anticlockwise for a single wire. Therefore, for the above set up the field lines contributed by the left wire will be in the upward direction and that contributed by the right wire will be in the downward direction.
The distance between the two wires is 2d and if we assume a point on the line joining the centres of two wires at a distance x from the left wire then its distance from the right one will be (2d-x).
Magnetic field at that point will be:
Bx=2πxμ0I+(−2π(2d−x)μ0I)=2πμ0I(x1−2d−x1)
The signs of the terms are based on the right hand thumb rule. At distance d from the left wire the point will be equidistant from the two wires and thus the net field at the midpoint will be zero. With this we can tell the correct options are either A or D since the other two have a non-zero value at midpoint. Now, on the left side of the left wire, the magnetic field from both the wires will add up in the downward direction and this negative, whereas on the right hand side of the wire on right, we will have a magnetic field adding up in the upward direction and thus positive sign. Option A shows all these above features and thus can be said as the correct one.
Note: You need not come up with the above expression. Since no numerical value is expected as an answer, you can reason the options out since the current in both wires are equal and the magnetic field lines cancel at the midpoint of the line joining both wires. Then signs of filed on either side of the wires can be deduced by the right hand thumb rule.
