Question
Question: Two long cylinders are arranged as shown to form overlapping cylinders, each of radius r, whose cent...
Two long cylinders are arranged as shown to form overlapping cylinders, each of radius r, whose centres are separated by a distance d. Current of density J flows into a plane of page along the right shaded part of page along the left shaded part of the other. The magnitude and direction of magnetic field at point O (O is the origin of x and y plane) are
(1)2πμ0πJd, in the +y direction.
(2)2πrμ0d2J, in the +y direction
(3)zero
(4)None of these
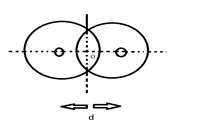
Solution
In the above question they are two cylinders, in which the current enters through one cylinder and leaves through the other cylinder. Apply Ampere circuital law on both cylinders separately. Ampere circuital law states the relationship between the magnetic and the electric field. Then by using the ampere’s circuital law we can determine the net magnetic field.
Formula used:
∫Bdl=μ0i
Hereμ0 is the permeability of the medium, i is the current enclosed by the closed path and B is the magnetic field.
Complete step by step answer:
Ampere’s circuital law states the relationship between the magnetic and the electric field.
According to the law, states that the product of current enclosed by the closed path and permeability of the medium is equal to the integral of (B) in an imaginary closed path.
Here the current enters through the right-side long cylinder and current leaves through the left side long cylinder. Then let us apply the Ampere’s circuital law on each cylinder.
It is given that Radius of the cylinders =r, Distance between their centres =d
Let us apply Ampere’s circuital law on the right-side cylinder
∫Bdl=μ0i
∫Bdl=∫Bdlcos0
(θ is 0 because B and dl are in same direction)
Also B is constant so we write B∫dl , where dl is equal to 22πd (Since r=2d ).
Hence, B22πd=μ0i
Also, i=(2)2jπ(d)2here jis the current density.
Now,B22πd=4μ0jπd2
On cancelling the term and we get,
B=4μ0dj
Applying the Ampere’s circuital law on the left cylinder we also get B=4μ0dj
Now the net magnetic field
Bnet=2B=2μ0dj
We can also write as
Bnet=2πμ0πdj, the magnitude of magnetic field and direction is along the + y direction.
Hence option (1) is the correct option.
Note: A magnetic field is generated, whenever a current travels through a conductor. The force will be zero, when the conductor is parallel to the magnetic field.
The force will be maximum, when it is perpendicular to the magnetic field.
The Magnetic field lines around a conductor carrying current are concentric circles whose centres lie on the wire. The Right-Hand Thumb Rule determines the direction of magnetic field lines.
