Question
Question: Two light strings of length \(4cm\) and \(3cm\) are tied to a bob of weight \(50gm\). The free ends ...
Two light strings of length 4cm and 3cm are tied to a bob of weight 50gm. The free ends of the strings are tied to pegs in the same horizontal line and separated by 5cm. The ratio of the tension in the longer string to that in the shorter string is:
(A). 4:3
(B). 3:4
(C). 4:5
(D). 5:4
Solution
The strings are attached to a horizontal support and tied to a bob. The forces acting on the bob must be the tensions in the strings and the force of gravity. Forces can be resolved into their components in perpendicular directions. Using Newton’s second law and making equations for forces acting in x-direction and y-direction, we can calculate the ratio by solving the equations and using properties of right-angled triangles.
Formulae used:
T1cosθ+T2sinθ=mg
T2T1=cotθ
cotθ=sinθcosθ
Complete step-by-step solution:
Given, two strings are tied to a bob. The system of strings and bob is isolated. Tension is a pulling force that acts along the axis. It operates in continuous objects like strings, rods, etc.
Resolving the forces acting on the system, we get,
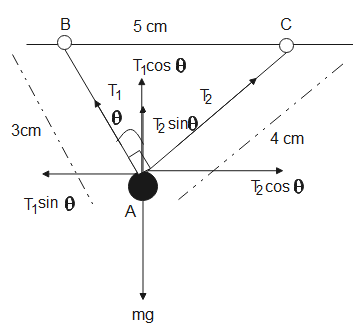
Since the triplet of 3cm,4cm,5cm is a Pythagorean triplet, therefore, ∠BAC=90o.
For forces acting in the y-direction,
T1cosθ+T2sinθ−mg=0
⇒T1cosθ+T2sinθ=mg - (1)
For forces acting in the x-direction,
T1sinθ=T2cosθ
∴T2T1=cotθ - (2)
We know that
cotθ=sinθcosθ - (3)
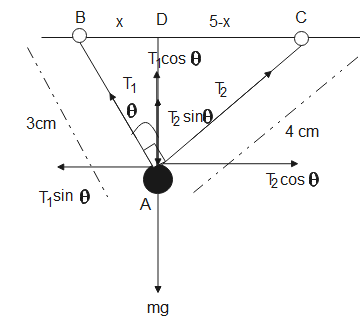
ΔABDcosθ=3AD
ΔACDsinθ=4AD
Substituting the above values in eq (3), we have,
cotθ=4AD3AD⇒cotθ=34
Substituting in eq (2), we get,
∴T2T1=34
Therefore, the ratio of the tension in the strings is 34. Hence, the correct option is (A).
Note:
Pythagorean triplet is a set of three numbers that obey the Pythagoras theorem. When a perpendicular is dropped from the opposite vertex to the hypotenuse, it divides it into two equal parts so it meets it at the midpoint. Forces acting in the opposite direction are subtracted. By Newton’s third law, tension acts equal and opposite on the string as well as on the object attached to it.
