Question
Question: Two lenses of focal length \({{\text{f}}_1} = 10cm\) and \({{\text{f}}_2} = 20cm\) are kept as shown...
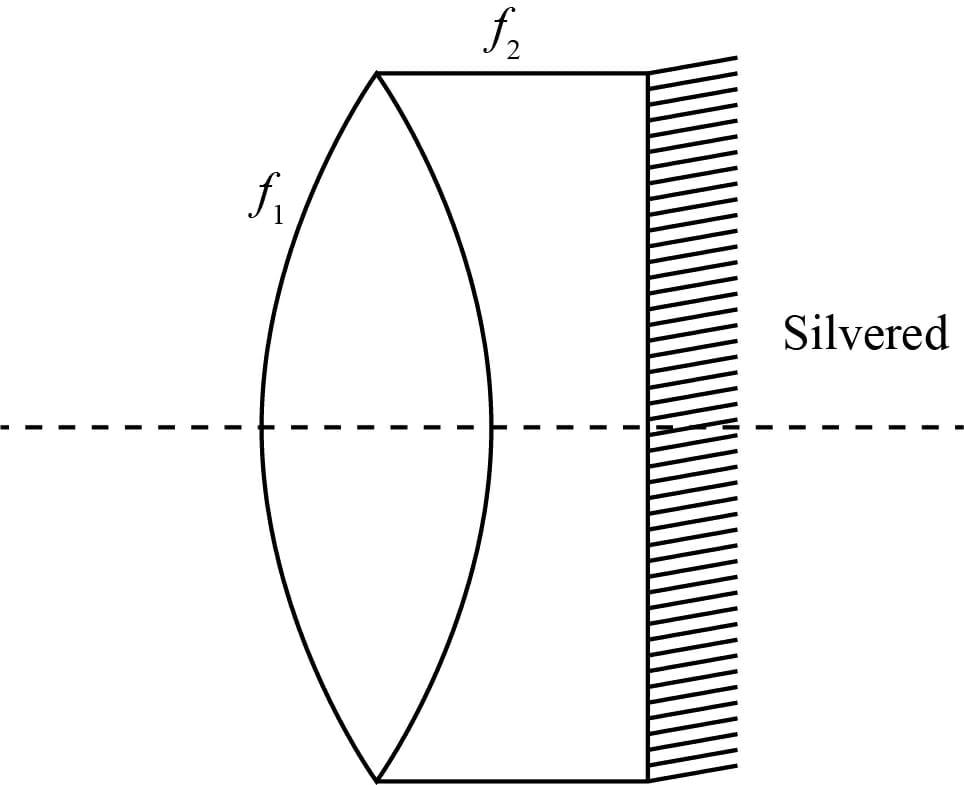
Two lenses of focal length f1=10cm and f2=20cm are kept as shown. The resultant power combination will be:
\eqalign{ & {\text{A}}{\text{. - }}10D \cr & {\text{B}}{\text{. }}5D \cr & {\text{C}}{\text{. - }}5D \cr & {\text{D}}{\text{. }}10D \cr}
Solution
Hint: As we know, the power of a lens is defined as the reciprocal of the wavelength, i.e.P = f1 . The unit of power of a lens is diopters (D). Here we find the power of the combination of a lens is the algebraic sum of the powers of the individual lenses in contact.
∴F1=f11+f21+........
Where f is a focal length.
⇒P = P1+P2+....
Complete step by step answer:
According to a given diagram
The focal length of the convex lens = 10cm
The focal length of the concave lens =−20cm
And the focal length of the plane mirror =∞
So, the resultant power of the combination of lens
F1=f11+f21+f31 ⇒F1=101−201−∞1
∴F1=201
⇒F = 20cm = 0.2m
Now the power of combination P = F1
⇒P = 0.21=5D
Additional information: The capacity of a lens to bend the rays of light depends upon the focal length. The smaller the focal length, the greater is the bending of a beam of light and vice- versa. Thus the power of a lens to bend the rays of light is inversely proportional to the focal length of the lens.
Note: If two lenses are separated by distance d meter, then the power of a combination of lenses is given by the relation
P = P1+P2−d.(P1.P2) Here d is the distance.
Always remember the power of a concave lens is negative, and the power of a convex lens is positive. We use a combination of lenses for higher magnification because lens combination multiplies each other's magnification power.
