Question

Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude $17.0\times {{10}^{-22}}C/{{m}^{2}}$.
What is E:
(a) in the outer region of the first plate
(b) in the outer region of the second plate and
(c) between the plates?

Answer 1

Firstly recall the Gauss law and hence understand that the electric field could be only present when there is a charge enclosed in the region. Electric fields will be zero for those regions that have no charge. Now recall the expression for the electric field due to thin sheets and then substitute to find the answer.
Formula used:
Electric field due to thin sheet,
$E=\dfrac{\sigma }{2{{\varepsilon }_{0}}}$

Complete answer:
In the question, we are given two large thin plates that are parallel and close to each other. We are also said that the surface charge densities of opposite signs and magnitude of $17.0\times {{10}^{-22}}C{{m}^{-2}}$is present on the inner faces of the given large thin plates. We are asked to find the electric field in three regions: (a) in the outer region of the first plate (b) in the outer region of the second plate and (c) in between the plates.

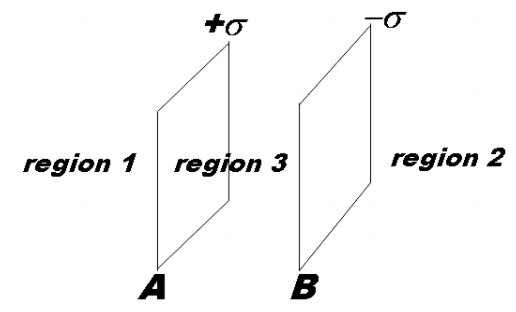
Let the surface charge density on the plate A be, $+\sigma =+17.0\times {{10}^{-22}}C{{m}^{-2}}$ and that on plate B be, $-\sigma =-17.0\times {{10}^{-22}}C{{m}^{-2}}$
(a) The outer region of first plate (plate A): region 1
As the surface charge densities are only present on the inner surfaces, by gauss law we know that a region devoid of charge will have no electric field. So the electric field here is,
${{E}_{1}}=0$
(b) In the outer region of second plate (plate B): region 2
Similar to the region 1, there is no charge enclosed in this region and so the electric field will be,
${{E}_{2}}=0$
(c) Between the plates A and B: region 3
We know that the electric field due to thin plane sheet of uniform charge density $\sigma$ is given by,
$E=\dfrac{\sigma }{2{{\varepsilon }_{0}}}$
${{\varepsilon }_{0}}=8.854\times {{10}^{-12}}{{C}^{2}}{{N}^{-1}}{{m}^{-2}}$
Here we have two plates, so the electric field in region 3 will be given by,
${{E}_{3}}=2\times \dfrac{\sigma }{2{{\varepsilon }_{0}}}$
$\Rightarrow {{E}_{3}}=\dfrac{\sigma }{{{\varepsilon }_{0}}}$
Substituting the values,
${{E}_{3}}=\dfrac{17.0\times {{10}^{-22}}}{8.854\times {{10}^{-12}}}$
$\therefore {{E}_{3}}=1.92\times {{10}^{-10}}N{{C}^{-1}}$
So the electric field between the plates is given by,
${{E}_{3}}=1.92\times {{10}^{-10}}N{{C}^{-1}}$

Note:
It is worthwhile to mention here that the electric field will be perpendicular to the surface. Even if the outer surface of the plates also had the same charge density, the net field would have been zero in regions 1 and 2. This is because the fields produced by both plates would have been oppositely charged and hence would have cancelled each other.