Question
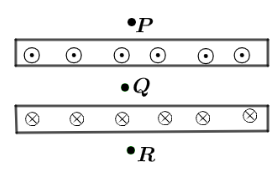
Question: Two large metal sheets carry surface currents as shown in the figure. The current through a strip of...
Two large metal sheets carry surface currents as shown in the figure. The current through a strip of width dl is Kdl where K is a constant. Find the value of the magnetic field at points P,Q and R.
Solution
In order to find magnetic field at points P,Q and R , we will use the ampere circuital law which is expressed as ∫B.dl=μ0I where I is the current flowing in wire and dl is the small section of area covered under magnetic field.
Complete step by step answer:
From the figure we can see that, current flowing in the upper strip is in upward direction whereas current flowing in the lower strip is in downward direction, so the magnetic field produced by each metal surface is in the opposite direction. Since, from symmetry we can say that the magnetic field at point P and R is the same.So, Magnetic field at point P and R from ampere circuital law is given as:
Current through each metal surface is KL and −KL,
Net current, Inet=KL−KL
Inet=0
Using ampere circuital law, ∫B.dl=μ0I
∫BP.dl=μ0Inet
Since, Inet=0
BP=BR=0
Hence, magnetic fields at point P and R are equals to zero.
Now, since point Q lies in the middle of two surfaces we will apply ampere circuital law between Q and R .
0∫LBQ.dl=μ0Inet
Since, current flowing in lower strip is in downward direction and has a magnitude of KL.So magnetic field at point Q is given by,
0∫LBQ.dl=μ0KL
BQL=μ0KL
∴BQ=μ0K In the right direction.
Hence, the magnetic field at point Q is BQ=μ0K .
Note: Ampere circuital law is applied when a current is flowing in wire and we need to determine magnetic field around it somewhere in space. μ0 Is called the permeability of free space and its SI unit is NA−2 and its numerical value is given as 4π×10−7NA−2.
