Question

Two lamps one rated $60W,\;220V$ and the other $40W,\;220V$are connected in parallel to a $220V$ electric supply mains. What is the total current drawn from the electric mains if the voltage of electric supply is$220V$?

Answer 1

We should check whether the bulbs are arranged in series or in parallel. We should know that voltage will be constant in a parallel circuit and current is constant in series circuit.

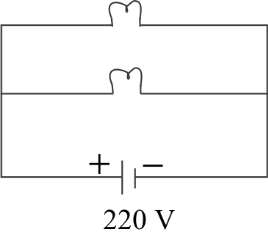
Complete step by step answer:
Parallel circuit is a closed circuit in which the current divides into two or more paths before recombining to complete the circuit.In parallel, both bulbs have the same voltage across them. The bulb with the lower resistance will conduct more current and therefore have a higher power dissipation and brightness. Most household electrical wiring bulbs are wired in parallel.

We have given two lamps in such way:
Power of ${I^{st}}$ lamp, ${P_1} = 40W$
Voltage of ${I^{st}}$lamp, ${V_1} = 220V$.
Power of ${2^{nd}}$lamp, ${P_2} = 60W$,
Voltage of ${2^{nd}}$lamp ${V_2} = 220V$
We know one thing.
${\text{Power = }}\dfrac{{{V^2}}}{R}$ [When potential difference is same then consider$P = \dfrac{{{V^2}}}{R}$]
So, resistance of ${I^{st}}$lamp, ${R_1} = \dfrac{{V_1^2}}{{{P_1}}}$
$= \dfrac{{{{\left( {220} \right)}^2}}}{{60}} = \dfrac{{48400}}{{60}} \\\ = 806.67\Omega \\\$
Resistance of ${2^{nd}}$lamp, ${R_2} = \dfrac{{V_2^2}}{{{P_2}}}$

$$= \dfrac{{{{\left( {220} \right)}^2}}}{{40}} = \dfrac{{48400}}{{40}} \\\ = 1210\Omega \\\$$

Now question said,
Both lamps are parallel.
So,
$\Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} \\\ \Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{806.67}} + \dfrac{1}{{1210}} \\\ \Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{{1210 + 806.67}}{{1210 \times 806.67}} \\\$
${R_{eff}} = 484\Omega$
Now, current drawn from electrical supply, i = potential difference/Req.
$= \dfrac{{220V}}{{484}} = \dfrac{{20}}{{44}} = \dfrac{5}{{11}}$

So, the correct answer is ${I_{total}} = \dfrac{5}{{11}}{\text{Amp = 0}}{\text{.4545Amp}}$.

Note:
In a parallel circuit, charge is divided up into separate branches such that there can be more current in one branch than there is in another. Nonetheless when taken as a whole, the total amount of current in all the branches when added together is the same as the amount of current at locations outside the branches.