Question

Two kids who are standing on different floors of an apartment block are dropping balls from the balconies. The second kid standing at the lower level drops the ball $2s$ after the first kid does. Both the balls reach the ground together. Calculate the heights between the two balconies? (Take $g=10m{{s}^{-2}}$)
$\begin{aligned} & A.20m \\\ & B.40m \\\ & C.80m \\\ & D.160m \\\ \end{aligned}$

Answer 1

First of all draw a diagram showing the details mentioned in the question. The displacement of the body is found by taking the sum of the product of the initial velocity and the time taken and the product of the half of the acceleration due to gravity and square of the time taken. This may help you in answering this question.

Complete step by step answer:

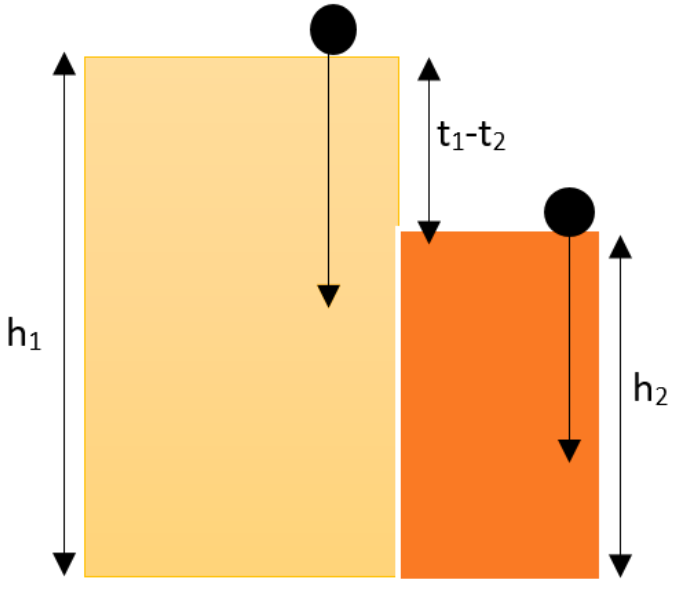
First of all let us mention what all are given in the question. The time difference between the fall of the ball is given as,
$\Delta t=2s$
Let us assume that the first ball is dropped from a height ${{h}_{1}}$ and the second ball is dropped from a distance mentioned as ${{h}_{2}}$. The time taken for the fall of the first ball can be mentioned as ${{t}_{1}}$which can be written as,
${{t}_{1}}=t$
And the time of fall of the second ball is mentioned as ${{t}_{2}}$which can be expressed as,
${{t}_{2}}=t-2$
The displacement of the body when it is moving is given by the equation,
$h=ut+\dfrac{1}{2}g{{t}^{2}}$
Where $g$be the acceleration due to gravity given as,
$g=10m{{s}^{-2}}$
The initial velocity of the ball when it is dropped is given as,
$u=0m{{s}^{-1}}$
Substituting the equation for the first ball can be written as,
${{h}_{1}}=u{{t}_{1}}+\dfrac{1}{2}g{{t}_{1}}^{2}$
That is,
${{h}_{1}}=\dfrac{1}{2}g{{t}^{2}}$
The application of the equation for the second ball can be written as,
${{h}_{2}}=\dfrac{1}{2}g{{\left( t-2 \right)}^{2}}$
The height difference between the initial positions of the ball will be,
${{h}_{1}}-{{h}_{2}}=\dfrac{1}{2}g\left[ {{\left( t \right)}^{2}}-{{\left( t-2 \right)}^{2}} \right]$
Simplifying the equation will give,

& {{h}_{1}}-{{h}_{2}}=\dfrac{1}{2}g\left[ {{t}^{2}}-{{t}^{2}}-4+4t \right] \\\ & \Rightarrow {{h}_{1}}-{{h}_{2}}=\dfrac{1}{2}g\left( 4t-4 \right) \\\ & \Rightarrow {{h}_{1}}-{{h}_{2}}=g\left( 2t-2 \right) \\\ \end{aligned}$$ Let us substitute the values in the equation, $$\begin{aligned} & {{h}_{1}}-{{h}_{2}}=10\left( 2\times 2-2 \right) \\\ & \Rightarrow {{h}_{1}}-{{h}_{2}}=20m \\\ \end{aligned}$$ **So, the correct answer is “Option A”.** **Note:** The velocity is defined as the rate of variation of the displacement of the body. The displacement is the shortest possible distance between the initial and final positions of the body. Both the quantities are vector quantities also which depends on both magnitude and the direction.