Question

Two isotherms are drawn at temperature ${T_1}$ and ${T_2}$ as shown. The ratio of mean speed at ${T_1}$ and ${T_2}$ is:

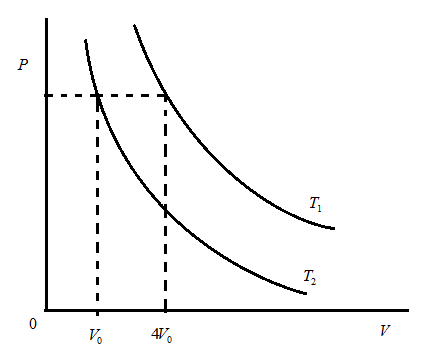
(A) $1:4$
(B) $1:2$
(C) $2:1$
(D) $4:1$

Answer 1

Here, the graph between pressure and volume is of isotherms at temperatures ${T_1}$ and ${T_2}$. We have to understand the meaning of isotherm in thermodynamics, a curve on a P-V diagram representing the state of a gas at constant temperature. Now, we have to use the terms shown in the above diagram and also the concept that volume is directly proportional to the root of temperature.
i.e. $V \propto \sqrt T$

Complete step by step solution:
Let us consider the above diagram as shown above:
Above graph is the isothermal graph which is between pressure and volume. This graph shows that there are two temperature curves of ${T_1}$ and ${T_2}$ .
In the isothermal process volume of the substance is directly proportional to the root of temperature such that $V \propto \sqrt T$ using this we are going to discuss about the ratio between two volumes such that:
$V \propto \sqrt T$
$\Rightarrow {V_1} \propto \sqrt {{T_1}}$ and ${V_2} \propto \sqrt {{T_2}}$
Now, we know that $PV = nRT$
From this we know that $T \propto V$
$\therefore$ The ratio between the volumes ${V_1}$ and ${V_2}$
$\Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{\sqrt {4{V_0}} }}{{\sqrt {{V_0}} }}$ … $\because \left( {{T_1} = 4{V_0},{T_2} = {V_0}} \right)$
$\Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \sqrt {\dfrac{{4{{{V}}_0}}}{{{{{V}}_0}}}}$
$\Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{2}{1}$
After solving all the equations above we concluded that ${V_1}:{V_2} = 2:1$
The ratio between the volumes is $2:1$
The correct answer is option C.

Note:
Here, we must understand the concept in isotherm that it is given by the change in volume but same in temperature. We have understood the concept that volume is directly proportional to the temperature by the ideal gas equation. We have to be careful about the calculation.