Question
Question: Two infinitely long uniformly charged rods are joined as shown in the figure. The linear charge dens...
Two infinitely long uniformly charged rods are joined as shown in the figure. The linear charge density on the rod is λ=LQ, Q is the total charge on each rod and L is the length of each rod. Find the electric field in vector form at point P due to the two rods.
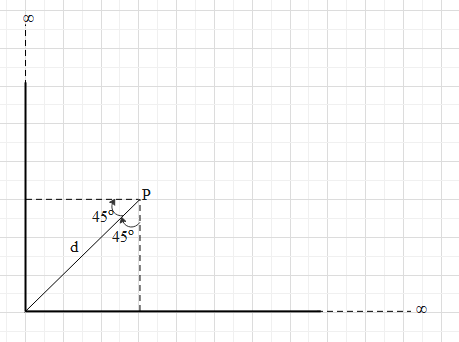
Solution
Understand how uniformly charged rod of some length produces an electric field at point P that is at a perpendicular distance d from the rod. Apply this formula for both the given rods and calculate the net electric field at point P.
Formula used:
Ex=4πε0dλ(sinθ1+sinθ2)
Ey=4πε0dλ(cosθ1−cosθ2)
Complete step by step answer:
Let them understand the electric field due to a charged finite rod.
Suppose a uniformly charged rod of linear charge density λ is placed vertically as shown. Then the electric field at a point P that is at a perpendicular distance d from the rod is given as:
Ex=4πε0dλ(sinθ1+sinθ2)
And
Ey=4πε0dλ(cosθ1−cosθ2)
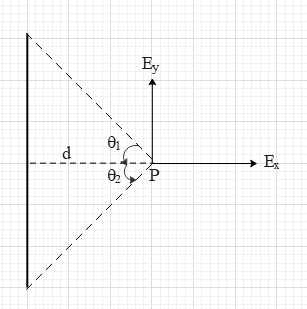
Here, Ex is the horizontal component of the electric field and Ey is the vertical component of the electric field.
θ1 and θ2 are the angles as shown in the figure.
Therefore, in vector form the electric field will be E=4πε0dλ(sinθ1+sinθ2)i+4πε0dλ(cosθ1−cosθ2)j
Let us now find the net electric field to the two rods as per arrangements shown in the figure of the question.
Let us find the electric field (E1) due to the vertical rod. For this rod, the perpendicular distance of the point P is dcos45=2d.
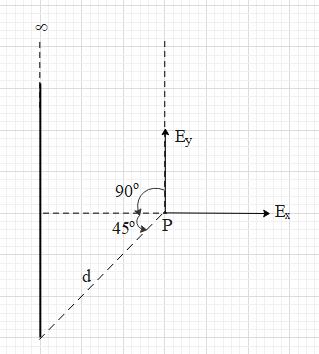
Since the rod is going up till infinity, θ1≈90∘.
From the figure, θ2=45∘.
Therefore,
⇒E1=4πε02dλ(sin90+sin45)i+4πε02dλ(cos90−cos45)j
⇒E1=4πε0d2λ(1+21)i+4πε0d2λ(0−21)j
⇒E1=4πε0d(2+1)λi−4πε0dλj
Let us find the electric field (E2) due to the horizontal rod.
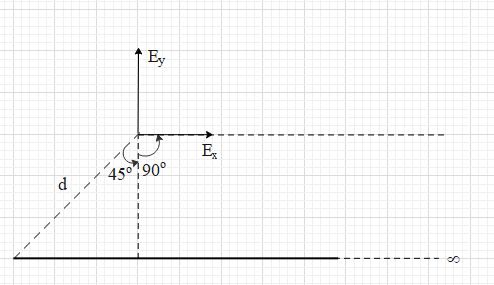
Here, the perpendicular distance is dcos45=2d.
θ1≈90∘ and θ2=45∘.
However, in this case the horizontal component will be Ex=4πε0dλ(cosθ1−cosθ2).
The vertical component will be Ey=4πε0dλ(sinθ1+sinθ2).
Since the data is same, we get that
E2=4πε0d−λi+4πε0d(2+1)λj
The net electric field at point P is E=E1+E1.
⇒E=4πε0d(2+1)λi−4πε0dλj+4πε0d−λi+4πε0d(2+1)λj
⇒E=4πε0d2λi+4πε0d2λj
⇒E=4πε0d2λ(i+j)
It is given that λ=LQ.
⇒E=4πε0dL2Q(i+j)
The above expression is the net electric field in vertical form at point P.
Note:
Note that the formula for the horizontal and vertical components of the electric due to a vertical rod is applicable only for a vertical rod. When the rod rotates by 90 degrees, the formula will change.
