Question

Two infinitely long straight wires lie in the $xy$-plane along the lines $x = \pm R$. The wire located at $x = + R$ carries a constant current ${I_1}$ and the wire located at $x = - R$ carries a constant current ${I_2}$. A circular loop of radius $R$ is suspended with its center at $\left( {0,0,\sqrt 3 R} \right)$ and in a plane parallel to the $xy$-plane. This loop carries a constant current $I$ in the clockwise direction as seen from above the loop. The current in the wire is taken to be positive if it is in the $+ \hat j$ direction. Which of the following statements regarding the magnetic field $\vec B$ is (are) true?
(This question has multiple correct options)
A. If ${I_1} = {I_2}$, then $\vec B$ cannot be equal to zero at the origin $\left( {0,0,0} \right)$
B. If ${I_1} > 0$ and ${I_2} < 0$, then $\vec B$ can be equal to zero at the origin $\left( {0,0,0} \right)$
C. If ${I_1} < 0$ and ${I_2} > 0$, then $\vec B$ can be equal to zero at the origin $\left( {0,0,0} \right)$
D. If ${I_1} = {I_2}$, then the $z$-component of the magnetic field at the center of the loop is $\left( {\dfrac{{ - {\mu _0}I}}{{2R}}} \right)$

Answer 1

In this question we need to determine which of the statements regarding the magnetic field $\vec B$ is (are) true. We will construct a figure according to the given question. Then, by using that we will consider each statement and determine the given statements are true or false.

Formula used:
Magnetic field can be calculated by the Biot savart’s law whose expression be given by $dB = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{Idr \times r}}{{{r^3}}}$
Magnetic field of straight wire along positive x-axis be given by the formula,
$B = \dfrac{{{\mu _0}I}}{{4\pi r}}\left( {sin{\theta _1} + \sin {\theta _2}} \right)$ $\widehat k$
where ${\theta _{1,}}{\theta _2}$ are the angles corresponding to the two ends of the wire.

Complete step by step answer:
Let us consider each statement and determine if the given statements are true or false.

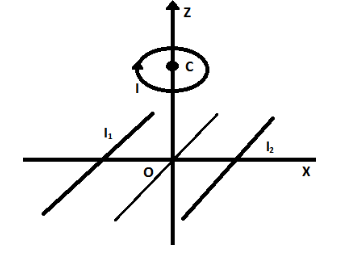
A. If ${I_1} = {I_2}$,
Magnetic fields along the two wires cancel each other at the origin. $\vec B = 0$ . Hence $\left( {{{\vec B}_{net}}} \right)$ at origin is equal to $\vec B$ due to the loop, which is non-zero. So, $\vec B$ cannot be equal to zero at the origin $\left( {0,0,0} \right)$.So, this statement is false.

B. If ${I_1} > 0$ and ${I_2} < 0$,
Magnetic field,$\vec B$ at origin due to straight line are along $+ \vec k$ direction (as ${I_1}$ is long the positive R direction) and magnetic field,$\vec B$ due to loop is along $- \vec k$ direction. Then $\vec B$ can be equal to zero at the origin $\left( {0,0,0} \right)$.So, this statement is true.

C. If ${I_2} < 0$ and ${I_1} > 0$,
Magnetic field,$\vec B$ at origin due to straight line will be along $- \vec k$ direction and magnetic field,$\vec B$ due to loop is along $- \overrightarrow k$ direction. Then $\vec B$ cannot be equal to zero at the origin $\left( {0,0,0} \right)$.So, this statement is false.

D. At center of loop, magnetic field, $\vec B$ due to the wires will cancel each other effect (as ${I_1} = {I_2}$) , then the magnetic field at the center of the loop is $\overrightarrow B = \dfrac{{{\mu _0}I}}{{2R}}\left( { - \widehat k} \right)$.So, this statement is also true.

Hence, correct options are B and D.

Note: It is important to note here that the electric current in a circular loop creates a magnetic field which is concentrated in the center of the loop than the outside. The magnetic field lines of the infinite wire are circular and centered at the wire, and they are identical in every plane perpendicular to the wire.